破甲弹破甲深度的计算是设计弹丸必然会遇到的问题，在建立破甲深度的计算公式之前，先讨论一下破甲过程中的一些基本现象，以及对破甲过程的力学分析。

1.金属流破甲过程的基本现象

金属流的破甲过程属于超高速冲击的范围，和一般穿甲弹相比，出现了许多新的现象和问题。

(1)金属流在破甲过程中逐渐消失

从金属流冲击靶板开始，随着破甲过程的发展，金属流逐渐失掉自己的能量。金属流一部分依附于穿孔的表面，少部分从入口处飞溅出去，当破甲过程结束后，金属流完全丧失原来的形状。金属流冲击靶板时，在接触面上产生很高的压力，并且压力随之逐渐降低。就紫铜金属流冲击合金钢板而言，金属流的绝大部分达到熔化状态，这样无论是飞溅出去的金属，还是依附于穿孔表面的金属，都是达到熔化状态的紫铜。

(2)被穿孔后的靶板质量基本不减

靶板经过金属流穿孔以后，尽管孔的容积不小，但实际上靶板的质量基本上不减。在破甲过程中，虽然有一部分金属流依附在穿孔表面，但质量很小。因此可以认为金属流的穿孔过程就是靶金属向侧向和前面流动的过程，并且主要是流向侧面，从入口和出口失掉的靶金属是极有限的。如果金属流对半无限靶作用，从入口飞溅出去的靶金属就更少了，一般不超过5%。

(3)靶板的穿孔呈圆锥形

由于金属流的速度从头部至尾部逐渐减小，当金属流破甲时，相应的入口孔径大，入口以后孔径依次减小，穿孔呈圆锥形。

(4)破甲的深度和孔径与靶板的强度有关

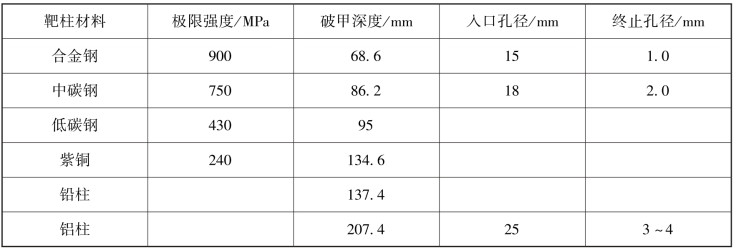
金属流穿孔的孔径远远大于金属流相应部分的断面直径，这主要是由于金属流的高速特性所致。金属流垂直破甲时，入口孔径通常为金属流直径的5~7倍，同种金属流的破甲深度和孔径取决于靶板的强度。表4.3.1列出了同一种聚能装药对几种不同材料靶柱的破甲情况。所用装药的直径为26 mm，炸药为梯黑50/50，紫铜圆锥形(40°)药型罩，罩厚为0.8 mm，炸高为60 mm。

表4.3.1　对不同材料靶柱的破甲数据

(5)穿孔周围形成一个硬化层

金属流破甲之后，穿孔的表面从入口到出口依附着一层金属流的金属。穿孔周围的靶金属由于经受金属流的强烈冲击，硬度普遍提高，形成了一定厚度的硬化层。紧靠穿孔靶面的靶金属，一般达到相变温度以上，再往里，温度越来越低。

2.金属流破甲的定常侵彻模型

因为射流的速度很高，在碰击靶板时，将产生很大的局部压力。在这种情况下，因冲击压力比靶板的强度高得多，靶板本身的强度可以不考虑。认为射流的速度是均匀的，侵彻速度也是不变的，将靶板也作为理想不可压缩流体处理。

设射流速度为vj，破甲速度为u，ρj、ρt分别为射流和靶板的密度。射流速度和侵彻速度之间的关系可表示为

破甲深度可表示为

这就是由定常理想不可压缩流体理论导出的破甲深度计算公式。该式表明，破甲深度P与射流长度l成正比，与射流和靶板密度之比的平方根成正比。此式与某些试验相符合，例如，增加炸高时，使射流长度l增加，只要射流不断裂和不分散，便能使破甲深度提高。又如，铜罩比铝罩的破甲深度深，这是因为铜罩的射流密度较大；铝靶比钢靶破甲深度大，因为铝靶密度小。公式还表明，破甲深度仅取决于射流的长度和密度及靶板的密度，而与靶板强度无关，甚至与射流速度无关。这是因为在建立公式时，假设靶板是理想流体，不考虑强度，射流有一点速度就能穿孔，这一点与实际情况是不符的。但是就射流头部来说，由于它的速度很高，忽略靶板强度的影响还是可以的。式(4.3.2)是在假设射流速度不变的条件下得到的，实际上射流速度是变化的，故要对它做修正。

3.金属流破甲的准定常侵彻模型(www.daowen.com)

实际的射流总是头部速度快，尾部速度慢，沿其长度方向存在一速度梯度，不具备定常侵彻条件，不能直接应用伯努利公式。但是就一小段射流来看，可以认为速度不变，因此可以应用伯努利公式，这就是准定常条件。

设射流速度沿长度是线性分布，射流头部到达药柱底部距离为b，H是炸高，破甲速度为u，射流速度为vj，最大破甲深为PM，破甲深度可表示为

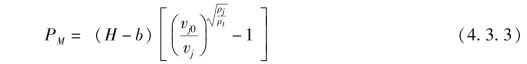
这便是准定常理想不可压缩流体的破甲公式，由该式可看出:

①破甲深度与H－b成正比，b很小时，破甲深度与炸高H成正比；

②射流头部速度vj0和尾部速度vj的比值越大，PM越大；

③射流和靶板的密度比越大，PM越大。

金属流形成之后，在空气中做惯性运动。由于运行距离不远，可以忽略空气阻力的作用。金属流从头部至尾部存在着速度梯度，在运行中它将不断地伸长，直至全部消耗为止。金属流伸长到某一定长度后，就由连续状态变为不连续状态，断裂为高速运动的金属颗粒。这就需要对这个破甲深度的计算公式进行修正，本书不再赘述。

4.破甲深度的经验公式

上述基于破甲理论的计算方法，不仅烦琐复杂，而且计算结果不精确。因此，在设计中采用简便的经验计算法有其一定的实用意义。这里介绍几个典型的经验公式，作为结构设计中初步估算破甲威力之用。

(1)根据现有制式装药结构总结的经验公式

这个经验公式是在定常流破甲理论基础上，根据制式装药结构的试验数据归纳整理而成

的静破甲深度公式，破甲深度为

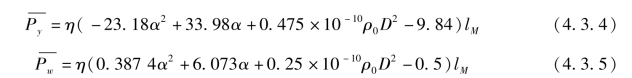
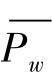式中，　为有隔板的静破甲平均深度；　为无隔板的静破甲平均深度；α为药型罩的半锥角；lM为药型罩的母线长；ρ0为装药密度；D为装药的爆速；η为考虑药型罩材料、加工方法及靶板材料对破甲的影响系数。

η取值见表4.3.2。

表4.3.2　η取值

(2)其他经验公式

对现有一些装药结构进行分析，总结了一些经验，归纳为以下一些经验公式:

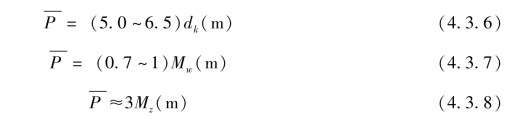
式中，dk为药型罩口部内直径；Mw为装药质量；Mz为药型罩质量。对柱状装药结构，取下限；对收敛形装药结构，则取上限。