力觉示教机器人是以人机协作为目标,通过人工牵引机器人末端手臂完成轨迹规划,实现机器人力觉示教控制。机器人控制系统是一个集运动学和动力学、耦合性、非线性的多变量为一体的控制系统。鉴于本身的多向控制,经典控制理论和现代控制理论在某种程度不能照搬使用。需要根据实际的工作情况,采取最佳的控制方式,从传统的编程自动化、微处理机控制到小型计算机控制等。

机器人在工业生产制造领域的应用大多只是简单的编程控制。示教方式相对单一,仅仅适用于多点单一路径的轨迹运动,面对一些复杂的轨迹控制,如不规则体的喷涂施釉、曲面打磨抛光、轴孔装配等工业工艺,机器人末端执行工具需要与工件之间产生接触力,此时,传统的逐点示教方式很难精确地实现既定轨迹示教,为了避免误差和提高机器人控制精度,需要机器人接触工件端拥有力觉反馈装置,使机器人末端执行器一方面能够沿着期望的运动轨迹执行,另一方面还要具备精确的接触力反馈,实时调整机器人的运动轨迹,最终完成复杂的工艺要求。

机器人运动学和动力学本身并没有涉及机器人与外界环境接触时的运算方式,但力是由两个物体接触时产生,故机器人的力控制问题其实是真实工作环境下所面对的接触力问题,也是轨迹规划控制问题。机器人需要像感觉器官一样的力反馈能力,使其在复杂操作面前能够很好地胜任。如果在机械手上安装力传感器,机器人控制系统就能够接收到末端力/力矩反馈信息,从而做出相应的运动指令调整,达到与接触环境相契合的控制程度。

机器人对外界环境约束的顺应能力称之为柔顺性。所谓柔顺控制,是指在机器人的末端执行工具与外部环境产生干涉的情况下,末端执行工具能够根据实际工况做出相应的轨迹调整。主动柔顺一般是通过改变控制器的方式,常见的是在机器人末端与法兰之间添加力传感器,增加力反馈控制,使机器人与工件之间能够完成柔顺的轨迹运动,使机器人控制更加智能化、轨迹运动更加精准。经典的机器人柔顺控制理论包括阻抗控制和力/位混合控制方法。

阻抗控制的这一概念是N.Hogan在1985年提出的。其特点是将工具速度和受力分别看作是阻抗和导纳,从而,机器人的力控制问题转化为阻抗与导纳的调节问题。所以,运用于机器人的阻抗控制其实是通过调节力和位移二者关系的控制方式,通过反馈调整位置误差、速度误差,从而间接完成机器人运动控制。具体的力作用关系式为

式中　

ΔX——位置误差;

Xd——名义位置;

X——实际位置;

K、B、F——弹性、阻尼、惯量系数矩阵。

图7-17所示为机器人力/位混合控制原理图。

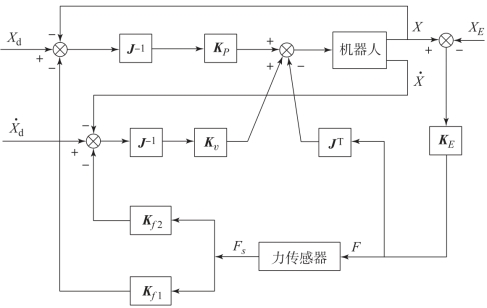
图7-17　机器人力/位混合控制原理图

刚度控制是以刚度系数Kp控制执行工具末端的位置和作用力的误差波动,表达式如下:

式中,Kp=diag [Kp1 Kp2…Kp6]。机器人随着矩阵Kp中的各个元素值的变化实现柔顺运动。

阻尼控制则是以阻尼系数Kv控制执行工具末端的速度和作用力之间的变量关系,表达式如下:

刚度控制和阻尼控制共同作用下实现了机器人与外界环境接触受力时,能够使机器人按照受力情况做出相应调整。

力/位混合控制作为经典的机器人主动柔顺控制策略,其控制原理是同时对力和位置进行控制。从所处空间关系来说,力和位置所在的空间是两个互补的自由空间,可以实现同步控制,且互不干扰,机器人各关节能够完成位置协调控制和对各自受力的平衡控制。机器人末端执行工具受到外力某个方向的作用力时,位置控制也在非受力方向进行位置坐标点控制,力信息反馈会对位置坐标做出更精确的定位,而位置控制又能为力控制提供具体的作用点,这种控制同时进行,相辅相成,最终达到力位混合控制的效果。

如图7-18所示,力/位混合控制是由位置控制和力控制两个独立的单元同时控制,此处借助雅可比矩阵建立关节变量和力/位之间的关系,从而驱动机器人完成指定轨迹运动。但该控制模式需要求解雅可比矩阵,对环境约束比较苛刻,且控制结构也会随之变化。

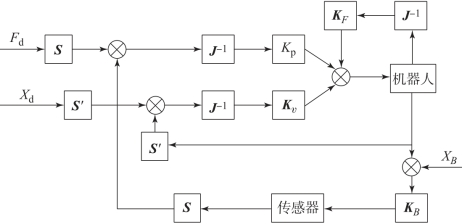
图7-18　机器人力/位混合控制原理图

在操作空间,机器人末端执行工具所受到的外力/力矩是力反馈示教的输入端,而通过算法转换得到的执行工具末端位置和姿态信息是输出端,控制机器人轨迹运动。所谓控制算法,就是外力/力矩数据和机器人执行工具位置和姿态变量的运算法则,两者之间是自变量和因变量的求解关系。假设外力/力矩用fT/mT表示,末端执行工具的速度变量用Δx(即Δv和Δω)表示,机器人在任意时间t的速度变量和角速度变量如下:

式中　Δv——机器人末端工具线速度变量;

kf——机器人末端受力运动灵敏度;

M——机器人末端工具质量。

式中　Δω——机器人末端工具角速度变量;

km——机器人末端受力矩运动灵敏度;

I——机器人末端工具转动惯量。

在实际机器人控制过程中,灵敏度kf和km可以根据实际情况设置,随时改变末端工具速度,使机器人末端运动与环境外力之间的转换更趋于柔顺,实现机器人更加智能的控制方式。

由式(7-38)可以确定机器人执行机构末端的位置矢量P;由式(7-39)可得到机器人末端姿态R;力觉示教机器人的末端执行机构的位置矢量P和姿态R分别为

式中: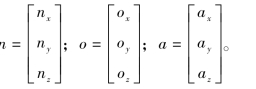

此处求解n,o,a需要用到RPY角法,通过力传感器获知的力矩信息可以分别确定绕x,y,z轴的旋转角度α,β,γ,故RPY旋转矩阵为

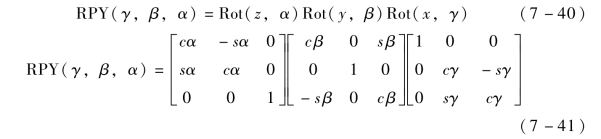
机器人轨迹示教最终是对关节驱动力的示教,不论是传统的示教盒示教还是离线示教,本质都是通过记录坐标点位置,以一种合适的机器人轴配置方式实现伺服电动机对关节转动的控制驱动。以六维力传感器为基础的机器人力觉示教,通过操作空间的力反馈信息,确定末端执行机构的位置和姿态,以一种不同于传统运动学逆解的方式获得关节空间转动角度以及各关节运动速度。

IRB2600机器人的最后三个关节为旋转关节而且轴线相交于一点,故其末端执行器的位置完全由前三个关节变量的大小决定,末端执行器的姿态则由后三个关节变量决定。

1.求解前三个关节角(www.daowen.com)

(1)求解θ1。根据机器人末端位置和姿态矩阵R分析,可得:

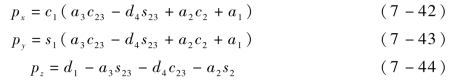
由于θ2,θ3还未求出,无法判断a3c23-d4s23+a2c2+a1的正负,故可能有以下两种情况:

①假设a3c23-d4s23+a2c2+a1>0,则有θ1的第一个可能解θ1a

②假设a3c23-d4s23+a2c2+a1<0,则有θ1的第二个可能解θ1b

(2)求解θ2。

根据式(7-42)、式(7-44)可得:

由式(7-50)套用三角代换公式可得:

(3)求解θ3。

为避免出现分母c1或s1为0,同样分两种情况讨论。

①若c1不等于0,用(7-47)和式(7-49)两式,整理得:

式中:w1=k1-a2c2,w3=k3+a2s2。

联立式(7-47)和式(7-48)两式,可求得:

故可求得:

②若c1等于0,用式(7-48)和式(7-49)两式,整理得:

式中:w2=k1-a2c2,w3=k3+a2s2。

联立式(7-58)和式(7-59)两式,求得:

故可求得:

2.求解后三个关节角

由齐次变换矩阵的构成可知,在计算运动学正解中求出的各个齐次变换矩阵的前三行和前三列即为对应的旋转矩阵,而且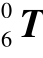和前三个关节角在前面已经求出,故可计算出:

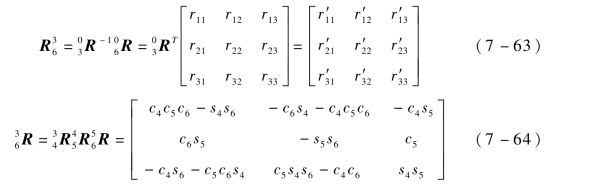
式中: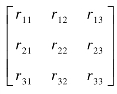表示执行器末端姿态R。

由以上两式中矩阵的对应元素相等,即可求得后三个关节角,具体步骤如下:

(1)求θ5。

由c5=r′23得:

(2)求θ4。

由-c4s5=r′23-c4s5=r′13及s4s5=r′33s4s5=r′33可 得:

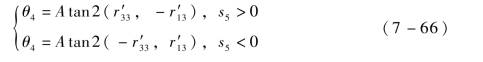
(3)求θ6。

由-c6s5=r′21及-s5s6=r′22可得:

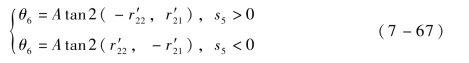
通过以上算法求解得到机器人各关节的变量关系,为后续实现轨迹运动做好铺垫,便于实时控制。