六维力传感器能够测量空间大小和方向实时变化的三个方向的力和力矩信息,一般安装在工业机器人末端,协助机器人完成力/位置控制、轮廓跟踪、轴孔配合等一些精细复杂的操作,在机器人中具有广泛应用。六维力传感器在随机器人运动的过程中,虽然传感器自身重力影响往往在其设计过程中已被考虑到并做相应处理,标定了使用前的初始零位值,使用时可以忽略传感器自身重力影响,但是,六维力传感器的另一端连接着操作工具,工具位姿的变化会影响工具重力作用在传感器各个方向的力/力矩值,传感器的零位值也会随之不断变化,这就导致传感器的测量产生一定偏差,降低了其测量精度,进而影响机器人的操作。因此,有必要对机器人运动中的六维力传感器进行重力补偿。

关于不同情况下的重力补偿,国内一些学者也分别进行过理论算法推导或相关实验研究等,并取得了一定的研究成果。谢光辉等人提出了一种利用最小二乘法的参数识别方法,可用于对机器人臂的重力补偿;林君健采用矢量分解的方法推导出一种机器人的重力补偿算法;李思桥等人提出的对机构的重力补偿理论计算是基于拉格朗日方程进行的,实现了对力觉交互设备的重力补偿。以上这些研究从不同出发点和落脚点,根据各自不同情况分析或推导了机械臂重力补偿的算法、验证及控制等问题,证明了重力补偿在机器人操作中的重要和必要性,对重力补偿研究具有一定的学习和借鉴意义。

本节针对机器人姿态变化导致末端工具重力影响六维力传感器零位值的问题,在结合前人研究的基础上,提出了一种方便有效的重力补偿算法,利用机器人各连杆的变换矩阵以及不同坐标系间的力坐标变换关系,消除六维力传感器测量过程中工具重力的影响,以便能实时补偿传感器的零位值,使传感器在机器人运动过程中能实时检测出末端工具实际所受外力的大小,从而使机器人能够完成更加精密的操作任务。

工业机器人在进行主动柔顺力觉示教过程中,机械臂的腕关节上会通过一个六维力传感器来连接末端执行工具,完成各项操作任务。传感器能够测得末端工具所受的外力/力矩,进而反馈给控制系统控制机器人实现柔顺运动。在这种情况下,为了消除工具自身重力对传感器示数造成的影响,得到准确的外力反馈信息,我们需要以机器人本体、六维力传感器、末端工具为研究平台,推导和研究相应的补偿算法对传感器测量结果进行重力补偿。

根据7.1.3中力坐标变换的建模原理,建立新的重力补偿模型,假设末端执行工具的重力大小为g,重心落在工具坐标系T的坐标原点,方向与空间基坐标系z轴的负方向一致,那么相对于空间基坐标系的重力分量矩阵恒为

通过式(7-16)、式(7-17)中的矩阵运算能够求解工具T坐标系相对于基坐标系在操作空间的位姿关系:

式中:

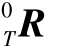是末端执行工具坐标系T相对于基坐标系{0}的旋转矩阵,联立公式(7-23)可得重力g在工具坐标系T下的矩阵变换:(www.daowen.com)

由于工具重心和坐标系T的坐标原点重合,故重力g在工具坐标系x,y,z三个方向的力矩为0,故具体的力(Tfg)/力矩(Tmg)变换如下:

那么由两坐标系之间操作力/力矩的坐标变换关系,可得重力相对于传感器坐标系S和工具坐标系T的变换矩阵如下:

根据式(7-17)可知,

由上式可知重力相对传感器坐标系S下的六维力/力矩,即对重力进行的重力补偿值:

机器人示教过程中,力传感器所检测到的力/力矩信息用fc、mc表示,通过重力补偿算法转换,末端执行工具所受的实际力/力矩信息用fs、ms表示,具体公式如下:

通过建立重力补偿模型,弥补了执行工具自身重力对六维力传感器实际测量结果所带来的误差,确保机器人末端位置和姿态变化时,能够捕捉到更精确的力/力矩信息,从而使机器人力反馈控制更加细腻,使机器人轨迹运动能够按照示教者意愿完美执行。同时,重力补偿模型的建立也为后续控制算法的研究做好铺垫。