IRB2600机器人结构尺寸如图7-3所示。该机器人由6个连杆依次连接,根据控制范围不同可以分为两组(第一组1～3关节,第二组4～6关节),第一组关节的转动用来确定机器人末端位置,第二组关节的转动用于末端姿态的确定。

机器人运动学分析通常是以数学方程式的形式来描述运动轨迹的,创建机器人固定基座与相邻连杆以及连杆之间的数学关系式作为机器人运动学分析的理论基础,求解末端工具的位置和姿态信息,确定各连杆关节旋转角度,完成运动轨迹规划[144～147]。机器人的示教技术(如遥控、离线、虚拟示教)都以此为依据展开创新研究。由于IRB2600机器人自身转动副衔接的连杆开链式结构,故可以将其转化成简单的旋转副驱动模型,通过各连杆已知的参数关系建立矩阵方程,用来描述各单位的相对位置关系和方向矢量。若想要完成机器人的运动规划,必然得构建相邻连杆的数学模型。

利用D-H坐标参数法建立机器人坐标系如图7-4所示,{x0,y0,z0}为基坐标系,相邻坐标系依次为{x1,y1,z1}、{x2,y2,z2}、{x3,y3,z3}、{x4,y4,z4}、{x5,y5,z5}、{x6,y6,z6},其他的机器人参数如连杆长度、扭角、关节角等如表7-1所示。

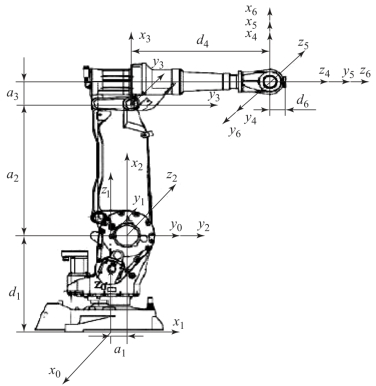
图7-4　机器人关节坐标变换示意图

表7-1　IRB2600机器人连杆参数表

D-H坐标参数法是一个通用的算式,适用于多关节机构。假设机器人有n个关节,那么就需要构建n+1个坐标系,D-H参数法就是通过坐标系之间的位置关系来确定机器人末端工具的位姿信息,加以实际机器人的连杆固定参数,形成一个适用于机器人运动学分析的通式:

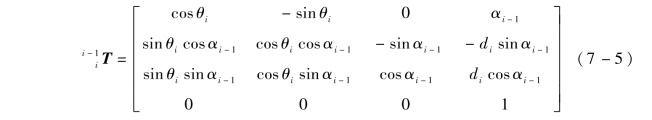
运动学正解是根据不同机器人的实际连杆几何尺寸和关节转角变量θ1,θ2,θ3,θ4,θ5,θ6,求得机器人执行机构末端位置P和姿态{n,o,a}的过程。将IRB2600机器人参数表内的数值代入D-H坐标参数法通用公式(7-5)中,得到以下6个变换矩阵关节(连杆i)1～6变换矩阵依次为

(www.daowen.com)

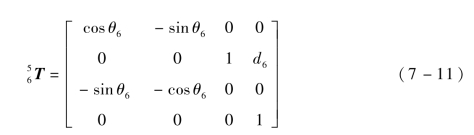
将6个变换矩阵依次相乘得到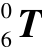,如式(7-12)所示,这就是执行工具末端相对基坐标系的位姿关系式。

当转动关节变量θ1,θ2,θ3,θ4,θ5,θ6发生变化时,机器人末端执行机构随之改变运动轨迹。此时末端位置和姿态关系式用矩阵R表示:

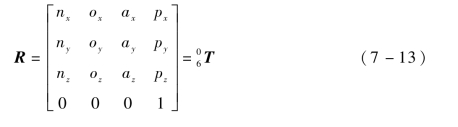
式中:

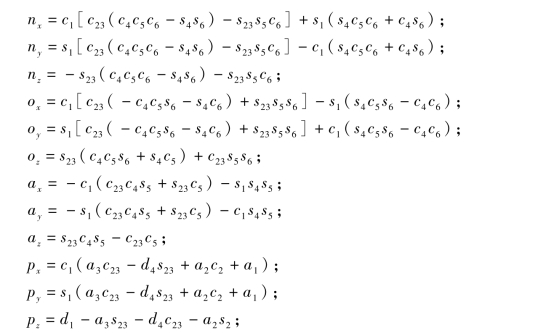
式中:ci=cosθi,si=sinθi,cij=cos(θi+θj),sij=sin(θi+θj)。

将机器人关节转动变量θ1=0°,θ2=-90°,θ3=0°,θ4=0°,θ5=0°,θ6=0°代入末端位姿矩阵R,验证执行工具相对于基座位姿关系的正确性。其计算结果如下所示。

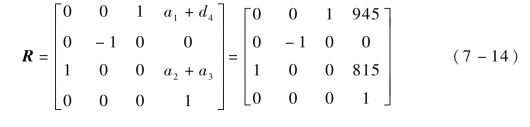
从计算结果中可以看到,位置数据与图7-4中的机器人结构尺寸完全相同,所以,该公式推导结果是正确的,可用于机器人运动学正向分析。事实证明,只要给出各关节具体旋转变量,就能求出机器人末端位置和姿态的唯一解,随着各关节的连续转动,进而形成一条完整的轨迹运动曲线,这也是机器人示教的本质原理。