由数学模型支撑的机器人运动学主要用于分析机器人各连杆的位置关系和各关节的转角变量,通过一系列的方程变换求解得到机器人的运动学运动参数[142～143]。如图7-1所示,主要包括以下两方面的分析:正向运动学求解和逆向运动学求解。

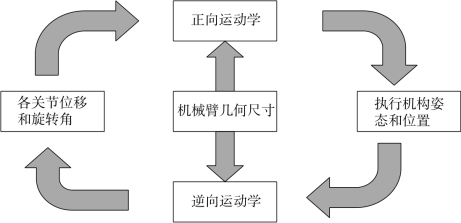
图7-1　机器人正逆学关系

(1)从机器人本体到操作空间的求解过程,一般称为正向运动学:由机器人各连杆的几何尺寸和各关节的转角变量作为已知量,构建与机械手末端位姿变量的数学关系式,必要的运动学数学坐标系方程是为了更加直观地呈现机器人末端手臂运动轨迹的位置和姿态信息,正运动学方程可以得到唯一解,每一次的转角变量都能确定唯一的末端位置和姿态变量,持续转动变量最终形成一条完整的运动轨迹,这就是机器人基于正运动学的工作原理。

(2)从操作空间到各关节的变换过程,一般称为逆向运动学:逆向运动学顾名思义,是把各连杆几何尺寸和末端工具位姿参数作为已知变量,通过建立数学方程式,求解各关节的旋转变量,逆运动学往往有多解并存的现象,这是因为不同的旋转变量可以满足同一条轨迹变量,因此机器人运动学需要进行轴配置,以确定最优旋转变量,快捷精准地完成轨迹规划。

描述机器人位置,首先建立机器人空间直角坐标系,机械臂末端在空间任意位置都能用3×1的位置矢量式来表达,假设空间中的一点用位置矢量P来表示,其公式表达如式(7-1)所示,Px,Py,Pz是该点位置x,y,z三个方向的分量。

机器人位置和姿态相辅相成,共同表达机器人所在工作空间的状态,通过直角坐标系确定P点位置后,还需要确定执行工具所处P点位置时的姿态,由于机器人是一个连杆机构,故需要数学方程求解各关节的位置和姿态信息,最终实现机器人运动。求解各关节位姿参数需要与固定基坐标系确立相对关系。(www.daowen.com)

图7-2所示为机器人活动坐标系B相对于固定坐标系A的变换示意图,三个方向的变换矩阵表示如下:

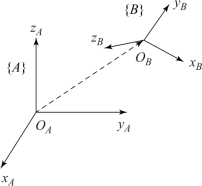
图7-2　坐标系变换

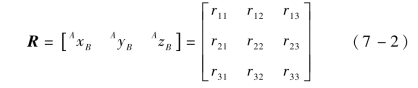
机器人相对位姿关系可用矩阵R表示,A是固定基坐标系,B是与固定基坐标系相连的连杆坐标系,AxB、AyB、AzB三个矢量是两两相互垂直的关系,故满足以下约束条件:

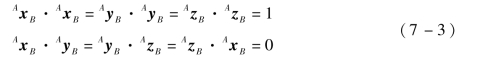
机器人的工作状态需要位置P和姿态R共同约束,用当前执行工具状态坐标系B{}来表示机器人运动轨迹的变化,即