1972年,Hawkins首先提出了一种运用对角优势矩阵的解耦方法,传感器补偿系统的传递函数是对角优势矩阵,以实现系统的近似解耦[139～141]。

设并联六维力传感器的传递函数是G(S),传递函数后面的定常解耦补偿网络为Kp,并联六维力传感器的传递函数用Q(S)=Kp×G(S)表示,上述方法的基本思想是使得Q(S)的每一行的非对角元的模之和都小于这一行的对角元的模,从而实现矩阵的对角优势化。

下面用MATLAB对并联六维力传感器解耦进行仿真。

为了验证以对角优势矩阵为基础的并联六维力传感器动态解耦的准确性,以此正交并联六维力传感器作为例子进行仿真分析,传感器的传递函数模型为

对于上述等式的传统函数模型,其解耦网络结构非常复杂,因此采用对角线优势补偿方法进行系统动态解耦研究。

运用MATLAB的SIMULINK仿真功能,搭建一个并联六维力传感器系统仿真图。在获得并联六维力传感器的系统仿真图后,将单位阶跃输入信号分别加载到通道1、2和3上,并获得并联六维力传感器的相应输出信号。

在并联六维力传感器的通道1上施加上述信号之后得到的输出信号如图6-12所示,由于并联六维力传感器受维间耦合的影响,主通道1的输出和输入完全不一样。因此,并联六维力传感器的输出进行对角优势矩阵解耦并且获得其输出信号,如图6-13所示。在解耦之后,并联六维力传感器的输出在很大程度上发生了改变,并且在轻微振荡之后主通道1上的输出稍微稳定在约2.2 V。同时,其他通道的输出显著降低,由此可得对角优势矩阵解耦之后效果较好。

图6-12　通道1的输出

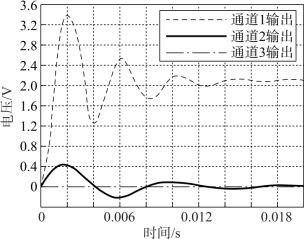
图6-13　通道1对角优势矩阵后的输出(www.daowen.com)

在并联六维力传感器的通道2上施加上述信号之后得到输出信号如图6-14所示。主通道2的输出和输入相比差别很大,因此,对并联六维力传感器的输出进行对角优势矩阵解耦,图6-15所示为获得传感器的输出。在解耦之后,并联六维力传感器的输出明显更好,并且在轻微振荡之后主通道2上的输出稍微稳定在约2.4 V。同时,其他通道的输出显著降低,表明解耦效果良好。

在并联六维力传感器的通道3上施加上述信号之后获得传感器的输出,如图6-16所示。主通道3的输出和输入相比完全不同。因此,并联六维力传感器的输出进行对角优势矩阵解耦,如图6-17所示获得传感器的输出。在解耦之后,传感器的输出明显改善,并且在轻微振荡之后主通道3上的输出稳定在约2.1 V。同时,其他通道的输出显著降低,表明解耦效果很好。

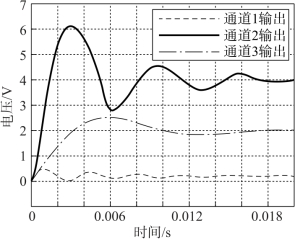
图6-14　通道2的输出

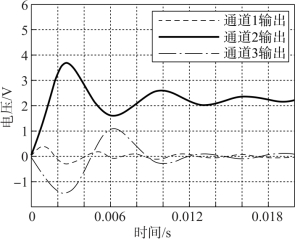
图6-15　通道2对角优势矩阵后的输出

图6-16　通道3的输出

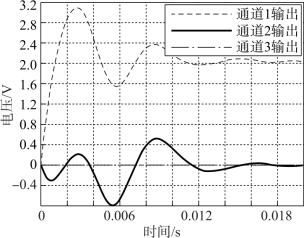
图6-17　通道3对角优势矩阵后的输出

从上述分析结果可以看出,通过对角优势补偿解耦后的输出信号在某种程度上是稳定的,它最后基本上稳定在约2.2 V,但是系统没有完全解耦。