在对获得的实验数据进行独立成分分析之前,我们需要预处理实验数据,如中心化和白化,从而使数据先进行一次简单的预处理。然后将预处理的实验数据进行分析,如图6-11所示。

ICA的向量矩阵模型为x=As。其中x={x1,x2,…,xn},s={s1,s2,…,sn}分别是观测信号和源信号,A={aij,i,j=1,2,…,n}是混合矩阵。

一般说来,ICA算法的选择基本上是在自适应算法和批处理算法之间。在自适应性的情况下,该算法通常通过随机梯度法获得,在这种情况下,所有独立分量都被同时估计。在批处理的情况下,有许多有效的算法。

对于多个分量的估计,按如下步骤操作:

(1)对观测数据X进行中心化,使其均值为0。

(2)对数据进行白化:X→Z。

(3)选择需要估计的分量个数m并且设置迭代次数p←1。

(4)选择一个初始权矢量(随机的)Wp。

(5)令Wp=E{Zg(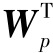 Z)}-E{g′( 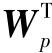Z)}W,非线性函数g的选择可以运用如下几种:

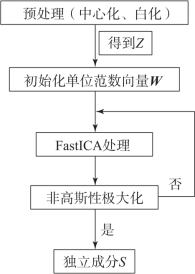
图6-11　ICA解耦流程图(www.daowen.com)

g(u)=tanh(au),1≤a≤2;g(u)=u∗exp(-bu2/2),b≈1;g(u)=u3。

(6)

(7)令Wj=Wp/‖Wp‖。

(8)假如Wp不收敛的话,返回第(5)步。

(9)令p=p+1,如果p≤m,返回第(4)步。

FastICA算法和其他的ICA算法相比:

(1)收敛所需要的时间短。

(2)可以使用任何非线性函数g直接找到任何非高斯分布的任何独立分量。

(3)通过选择合适的非线性函数g可以优化其性能。

(4)可以逐个估计独立分量,类似于进行投影跟踪,如果只需要估计几个独立分量,则可以减少计算量。

(5)FastICA算法有许多神经算法的优点:并行以及分布式计算,简单计算,内存需求较低。