独立成分分析(Independent Component Analysis,ICA)是一种计算方法和统计技术[126～128]。我们假设这些内在变量是非高斯的并且彼此独立,我们将它们称为观察数据的独立分量,这些独立成分能够经过ICA方法找到[129～131]。

本节主要介绍了独立成分分析(ICA)理论,并阐述了ICA在不同条件下的仿真,证明了ICA有利于多维传感器的解耦。

鸡尾酒问题:假设在房间中,有m(m>1)个人在同时讲话,还有n(n≥m)个麦克风,摆放在不同的位置进行记录。n个时间信号用xn (t)表示,信号幅值用xn表示以及时间变量用t表示。

上述情况可用如下方程表示:

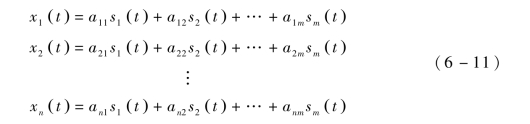
式中,aij(i=1,…,n,j=1,…,m)是由麦克风和扬声器之间的距离决定的参数。xn(t)用列向量X表示,sm (t)用列向量S表示,矩阵A表示系数,上述方程写成矩阵形式为

ICA问题是:根据随机观察数据X、估计混合矩阵A和源信号S。在估算混合矩阵A之后,计算混合矩阵的逆即分离矩阵W=A-1,以便可以获得独立分量S的估计值为

独立成分分析(ICA)过程实际上是建立目标函数来进行优化从而达到近似的目的。ICA的数学模型如图6-10所示。ICA的向量矩阵模型为

X=AS(www.daowen.com)

式中,X={x1,x2,…,xn },S={s1,s2,…,sn }分别为观测信号和源信号,A={aij,i,j=1,2,…,n}为混合矩阵。

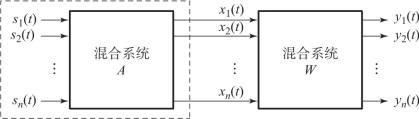
图6-10　ICA的数学模型

未知的源信号以及混合矩阵用图6-10中的虚线来表示,ICA的出发点就是假设源信号s,彼此相互独立,通过建立以独立性为基础的目标函数,建立分离矩阵W和混合矩阵A,由此估算出源信号为y=Wx=WAS=GS,当G=I时就实现了对源信号的完全估计。

ICA算法包括三个主要的方面:中心化、白化和独立成分分解。中心化是ICA简化的第一步,白化是第二步。经过处理的信号x满足cov(x)=I,E(xxT)=I,称为白化信号。假设x为观测信号,白化矩阵为:Q=ED-1/2ET,式中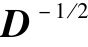=diag (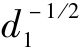,…,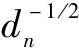)。对观测信号进行白化处理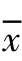=Q·x=Q·AS=。

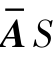ICA中独立成分分析的估算方法包括两个方面:建立目标函数(优化准则)和优化算法。目标函数可以选择峭度、熵、互信息和这些定义的变体。优化方法包括最大似然估计、快速ICA算法等。在定义了目标函数的基础上,ICA可以表述为:首先,利用信息论等方法创建以分离矩阵W为变量的目标函数J(W),当J(W)取得极值时的W即为所求。其次是寻找一种有效的算法求解W。

概率论中的一个定理称为中心极限定理(Central Limit Theorem),它讨论了随机变量序列的部分和在正态分布中的分布,是数理统计和误差分析的理论基础。

定理:设随机变量序列x1,x2,…,xn彼此独立并且遵循相同的分布,E {xk}=u,D {xk}=σ2≠0,k=1,2,…,则随机变量的分布函数Fn (x)满足

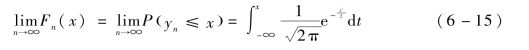
由上面的公式可以看出,当n趋向于时,随机变量yn→标准正态分布N (0,1)。因此,当n足够大时,具有相同分布的n个独立随机变量x1,x2,…,xn的总和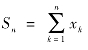几乎遵循正态分布N (nμ,nσ2)。