为了验证上述推导结果的正确性,本节采用数值实例进行分析。首先,假设Stewart并联结构六维力传感器的结构参数为:R=100 mm,r=60 mm,h=70 mm,α=π/2,β=π/6。

根据以上结构参数,求得传感器初始状态的一阶静力影响系数矩阵为

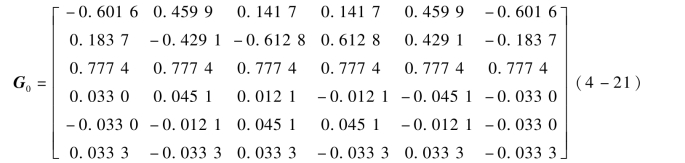
假设传感器测量分支的刚度系数相同,均为k=2.8×105 N/m,传感器的力与力矩量程分别为Fx=Fy=Fz=±100 N;Mx=My=Mz=±5 N·m。

当作用在传感器上的力为Fx=100 N时,由式(4-20)得到考虑分支变形的传感器的一阶静力影响系数矩阵为

在ADAMS软件中建立Stewart结构六维力传感器模型,在传感器上平台沿x轴方向施加100 N的力,此时可测得各测量分支中产生的反作用力,代入式(4-14)中可分别计算出考虑测量分支变形前后传感器能够检测的六维力,将结果列于表4-3中。

表4-3　施加Fx=100 N时传感器的测量结果

由表4-3可看出,经过考虑测量分支变形进行补偿后,传感器的受力方向以及耦合方向的检测精度得到一定提高,从而验证了该补偿方法的可行性与正确性。(www.daowen.com)

下面分析传感器由测量分支结构变形引起误差的影响因素。传感器的测量误差可由下式确定

式中,Fs为六维力的理论值;Fc为六维力的测量值;Fm为传感器的满量程力或力矩。

将考虑测量分支变形补偿前后得到的测量值Fc代入式(4-23)中,可分别得出补偿前后传感器的测量误差。由式(4-19)可看出,测量分支变形对传感器引起的误差与测量分支刚度系数和外力大小有关,图4-34所示为传感器的测量误差随外力大小以及分支刚度的变化曲线。从图4-34中可知,在所假设的Stewart并联结构参数下,当测量分支刚度大于106 N/m时其变形对测量误差的影响是很小的;另一方面,该误差与外力的大小直接相关,当外力增大时测量分支变形会变大,进而引起的误差也会变大。

图4-34　测量误差随外力大小以及分支刚度的变化曲线

当测量分支刚度为2.8×105 N/m时,通过计算得到了施加六个方向力/力矩时由分支变形引起的测量误差,如图4-35所示。经过对测量分支变形补偿前后所得误差的比较可看出,所提出的补偿算法可有效地减小由于测量分支变形引起的误差,进而提高传感器的测量精度。另外由上述计算和仿真也可看出,对于一般的并联结构六维力传感器来说,当测量分支刚度很高、量程不大的情况下,其结构变形对传感器测量精度影响很小,从而也验证了多分支并联结构用于六维力测量的可行性。

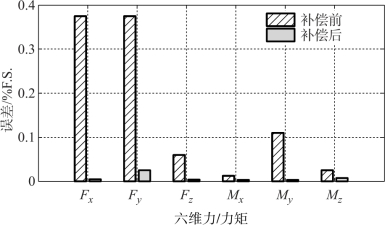
图4-35　补偿前后六维力传感器各方向测量误差