当有外力作用在传感器上平台时,六个测量分支产生反作用力,因此各测量分支会响应产生一定的轴向变形。由于对于Stewart并联结构而言,各平台的刚度要远远大于分支刚度,因此平台的变形相对于测量分支而言可以忽略。测量分支轴向变形会导致上平台位姿发生变化,如图4-33所示。

由各测量分支所产生的反作用力与其轴向变形之间的关系,综合所有测量分支并整理成矩阵形式,可得

图4-33　测量分支受力变形示意图

式中,Δl=[Δl1Δl2Δl3Δl4Δl5Δl6]T;K=diag(k1,k2,k3,k4,k5,k6)。

假设由测量分支轴向变形会引起上平台位姿变化为ΔD,并将其写为如下形式

式中　Δd——位置变化矢量;

Δθ——姿态变化矢量。

由Stewart并联机构运动学,可得测量分支轴向变形与上平台位姿变化之间的映射关系为(www.daowen.com)

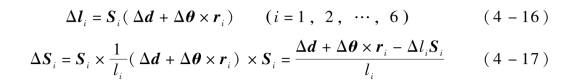
式(4-16)表达了第i个测量分支的轴向变形与上平台位姿变化之间的关系,将六个测量分支综合到一起写成矩阵的形式为

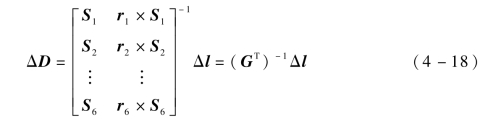
将式(4-14)代入式(4-18)中,可得

根据式(4-19),当有外力作用到传感器上时,可由测量分支所受轴向力得到传感器上平台位姿变化。此时,传感器所受六维外力与测量分支轴向力之间的映射关系可写为

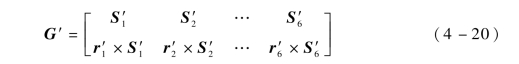
式中,S′i=Si+ΔSi;r′i=ri+ΔliSi;r′i×S′i=(ri+ΔliSi)×(Si+ΔSi)=ri×(Si+ΔSi)。

将式(4-16)、式(4-17)代入式(4-20)中,可得到考虑测量分支变形后的传感器一阶静力影响系数矩阵。

由于测量分支受到轴向力后会产生一定的变形,进而导致传感器的输入输出关系矩阵发生变化。然而,测量分支轴向变形是与其受力有关的,因此需要实时计算矩阵G′来补偿分支变形对其映射矩阵的影响。映射矩阵G′相比未考虑分支变形的初始矩阵G更加接近实际情况,因此可以降低测量分支轴向变形所带来的测量误差。