【摘要】:本节对传统Stewart结构六维力传感器进行误差分析,因此分析结果更具普遍性意义。图4-32Stewart并联结构六维力传感器示意图首先建立Stewart并联结构六维力传感器的数学模型,如图4-32所示。Stewart并联结构六维力传感器由上平台、下平台以及六个弹性测量分支组成,测量分支两端与平台通过球副连接。式中,映射矩阵G称作传感器的一阶静力影响系数矩阵,可表示为
本节对传统Stewart结构六维力传感器进行误差分析,因此分析结果更具普遍性意义。
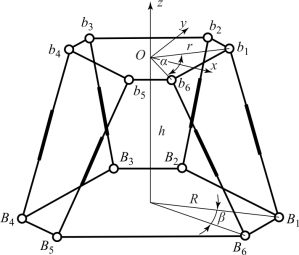
图4-32 Stewart并联结构六维力传感器示意图
首先建立Stewart并联结构六维力传感器的数学模型,如图4-32所示。Stewart并联结构六维力传感器由上平台、下平台以及六个弹性测量分支组成,测量分支两端与平台通过球副连接。图4-32中,Bi (i=1,2,…,6)表示下平台球铰点中心;bj (j=1,2,…,6)表示上平台球铰点中心,且在上下平台平面内相邻两个球铰点与中心连线夹角均为120°。传感器的测量基准坐标系Oxyz原点建立在上平台中心,x轴、y轴在上平台平面内,且x轴垂直于球铰点b1、b6连线,z轴竖直向上。R表示下平台球铰点到下平台中心距离;r表示上平台球铰点到上平台中心距离。α表示上平台平面内球铰点b1、b6与中心连线的夹角;β表示下平台平面内球铰点B1、B6与中心连线的夹角;h表示上下平台之间的高度,li (i=1,2,…,6)表示各测量分支长度。
当有六维力作用在传感器上平台时,可由螺旋理论求得上平台静力平衡方程,可表示为
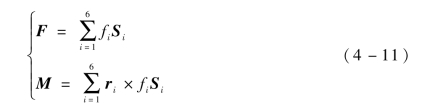 (www.daowen.com)
(www.daowen.com)
式中,F和M分别为作用在传感器上平台的作用力和力矩;ri为测量分支轴线一点在坐标系Oxyz中的位置矢量;Si和fi分别表示第i个测量分支方向矢量和测量分支所产生的反作用力。
式(4-11)可改写为矩阵形式为
![]()
式中,Fw=[Fx Fy Fz Mx My Mz]T;f=[f1 f2…f6]T。
式(4-12)中,映射矩阵G称作传感器的一阶静力影响系数矩阵,可表示为
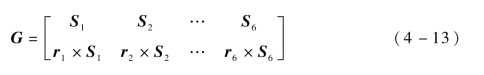
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关正交并联六维力传感器及其应用研究的文章







