广义并联多分支六维力传感器一般由三个主要部分组成,分别为测力平台、固定平台以及测量分支,其结构示意图如图2-1所示。将坐标系Oxyz建立在测力平台上作为基础坐标系。测力平台上的分支球铰点b1,b2,…,bn对于基坐标系的空间位置用矢量b1,b2,…,bn表示,固定平台上的分支球铰点B1,B2,…,Bn对于基坐标系的空间位置用矢量B1,B2,…,Bn表示。

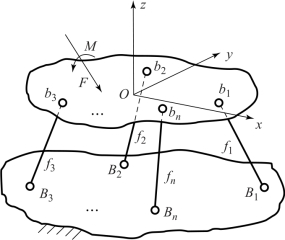
图2-1　广义并联多分支六维力传感器结构示意图

基于螺旋理论,建立测力平台的静力学平衡方程,有

式中　F,M——施加在传感器测力平台上的空间作用力和力矩;

fi——分支i在测力平台传递的外力作用下产生的轴向力;

$ i——分支i的轴线在基准坐标系中的单位线矢,有$ i=Si+∈S0i,Si·Si=1,Si·S0i=0,S0i=ri×Si;ri为分支i的轴线上某一点的位置矢量。

将式(2-4)改写为矩阵的形式有(www.daowen.com)

式中　Fw——作用在测力平台上的空间三维外力和空间三维外力矩组成的六维外力矢且Fw=[Fx Fy Fz Mx My Mz]T;

f——由测量分支轴向力所组成的向量,f=[f1 f2…fn ]T;

G——测量分支轴向力到空间六维外力的映射系数矩阵,维数为6×n,可将其写为

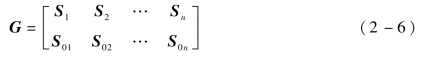
将各球铰接点对应的坐标向量代入,则式(2-6)可表示为

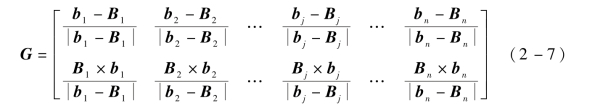
将fn看作未知数,在传感器结构非奇异,即G的列向量不相关时,静力平衡方程有解。此时若n=6,则静力平衡方程有唯一解,即有唯一的测量分支轴向受力fn与空间六维力Fw对应;若n>6,测量分支数大于使测量平台达到静力平衡的最小数目,则传感器为超静定结构,静力平衡方程有无穷多解,即有多组测量分支轴向力fn可与六维力Fw平衡,此时需引入广义逆矩阵来求解测量分支轴向力。伪逆矩阵是广义逆矩阵的一种,由于它具有唯一性,这里引入伪逆矩阵来对并联结构六维力传感器的静力平衡方程进行求解。