选择从区域水资源系统稳定性的角度,来研究区域水资源可持续利用预警系统是基于这样的考虑,一方面,稳定性对于任何一个系统都非常重要,不稳定通常会产生自发的灾变,区域水资源系统也不例外。区域水资源可持续利用预警系统的研究目标就是要预报和预防这种灾变的发生,因此区域水资源系统稳定性的分析就成了区域水资源可持续利用预警的重要内容和基本手段。另一方面,人们对区域水资源系统控制的目的就是要使区域水资源系统在状态空间中的描述点保持在一定的许可区间内,预警系统恰如其分地体现了这种系统的控制目的,而系统的稳定性就是描述和度量这种控制目的的一个基本概念。

区域水资源系统是一个非平衡开放系统,其物质循环、能量流动和信息传递能较长时间地保持稳定状态,并对内部和外部的干扰有一负反馈机制,使得干扰不致破坏系统的稳定性,但当这种干扰超过其所能忍受的阈值时,系统就会崩溃瓦解即发生突变,这种突变需要预先报警,而突变论又为预警的实现提供了定量化的数学手段。

区域水资源系统是一个动态的复杂系统,总是处在动态的发展变化过程中；而且在一定的时间和相对稳定的条件下,总是趋向稳定有序的发展方向即在动态中维持平衡。区域水资源系统的不稳定因素不计其数,但主要来自两个方面,其一是系统内部自激 (Self Generating)的不稳定因素,其二是环境施加的干扰因素。这两类因素的叠加和积分迫使区域水资源系统的状态发生变化；如果这种变化发生在一定的阈值内,系统通过与环境的物质、能量和信息的交换、通过内部的自组织和自调节可以恢复到原始状态,并使系统向稳定有序的方向发展；如果这种变化超过一定的阈值,也就是突破稳定性的临界点,就会引起区域水资源系统的生产力衰退、结构功能失调、物质循环和能量交换受阻,最终导致系统的歧化、退化、甚至崩溃。

区域水资源系统稳定性的临界点就是预警系统中需要确定的警限即有警或无警的分界线,它是预警分析的核心和焦点。区域水资源系统稳定性的预警分析如图3.11所示。

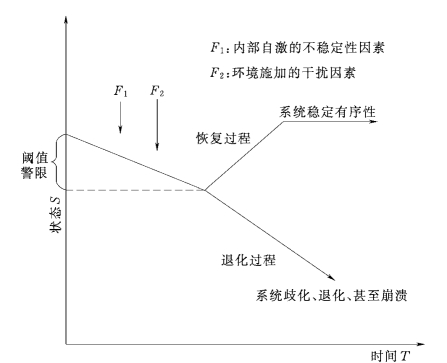
图3.11　稳定性的阈警分析示意图

3.4.2.1　稳定性的概念

稳定性(Stability)是对外界干扰的区域水资源系统振荡的幅度和频率,恢复的过程和时间的辨别,是指受外界干扰后,系统抵抗偏离初始态的能力和通过内部调节恢复到初始态的能力。稳定性是区域水资源系统生产力可靠性和恒定性的反映,也是系统缓冲能力的反映,还是系统自组织、自调节和自适应性的集中反映。稳定性概念可以用数学语言表达为:

式中:Δx(t)是系统被调量与平衡的偏差值；ε是任意小的规定量。

如图3.12所示。

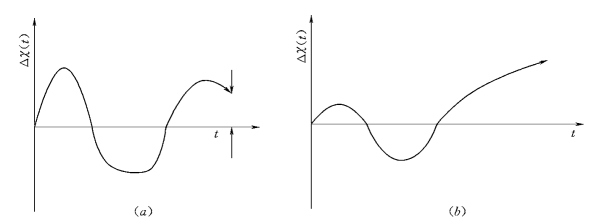
图3.12　稳定性概念示意图

(a)稳定系统；(b)非稳定系统

区域水资源系统稳定性的类型很多,这是因为系统对外界干扰的反应和恢复过程各不相同,其类型如图3.13所示,主要类型有:持续稳定性即系统对于干扰影响的反作用强烈,在干扰发生后短时间内或正在面临干扰时,也能维持或接近系统原来的状态；阻尼稳定性即系统遭到干扰时,自行增强抗干扰能力,系统状态只发生微小的循环振荡,便迅速恢复原状；循环稳定性即系统受到干扰后,表现出较大振幅的循环振荡；弹性稳定性即受到干扰后,表现出大振幅的循环,当干扰因素消除后,系统逐渐恢复到原来状态。

3.4.2.2　稳定性的评价

人们为了测度区域水资源系统所处的状态,提出了稳定性概念。稳定性问题很早引起人们注意,Ckements和Shelford(1939),Odum (1953)和Mac Arthur(1995)等人对生态系统稳定性问题进行过研究,但20世纪70年代中期以前,主要集中在稳定性的一般理论研究。稳定性评价活动始于70年代,Gardner等人 (1970)提出测度稳定性的连接度(Connectance)概念。O.Neill(1976)对苔原、池塘等六个不同生态系统受干扰后返回平衡点的时间作过定量测度。稳定性评价指标主要有:恒定度 (Constancy)、持久度(Persistence)、脆弱度 (Vulnerability)、惯性 (Inertia)、弹性 (Elasticity)和振幅(Amplitude)等,但是用于定量评价区域水资源系统稳定性的指标却很少,根据我们初步的归纳总结主要有:

(1)系统产出扰动度(O′):

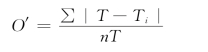
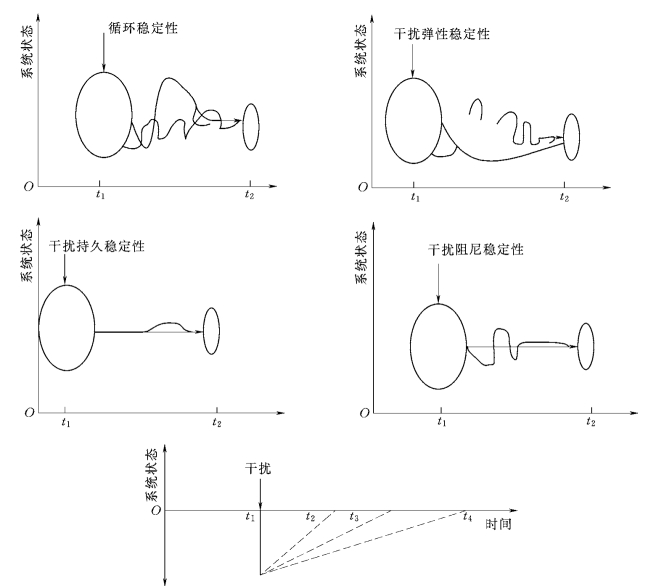
图3.13　稳定性类型示意图

式中:n为计算期年数；Ti为计算期内第i年产出量；T 为计算期内平均年产出量。

(2)系统输入扰动度(I′):

式中:n为计算期年数；C 为计算期平均年输入量；Ci为计算期内第i年产出量。

(3)系统产值优势度(C):

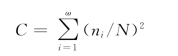
式中:ni为第i子系统产量值(量)；N 为系统总产值(量)；ω 为系统子系统个数。

(4)稳定性综合指数(S):

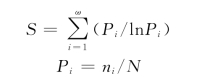
式中:Pi为第i年子系统产值优势度；N 为系统总产值；ni为第i子系统产值；ω 为系统子系统个数。

(5)系统产值离异度(δ):

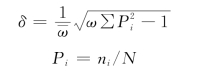
式中:Pi为第i年子系统产值优势度；N 为系统总产值；ni为第i 子系统产值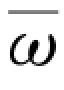；为系统子系统个数。

(6)系统受容度(C):

式中:B 为系统生物量；K 为系统生物容纳量。

(7)系统产值振动度(D):

式中:P 为系统年产值；P为计算期平均值。

(8)交叉替代结构弹性(EC):

式中:Qx1为结构组分X 的期初量；Qx2为结构组分X 的期末量；Qy1为结构组分Y 的期初量；Qy2为结构组分Y 的期末量。

(9)收入弹性系数(F):(www.daowen.com)

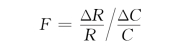
式中:R 为现期价格,C 为现期成本；ΔR,ΔC 为现期与基本之差。

(10)输出弹性系统(ES):

式中:Q1为期初输出量；Q2为期末输出量；P1为期初价格；P2为期末价格。

尽管上面提出了这些可以量化的区域水资源系统稳定性的评价指标,但目前要想通过它们进行区域水资源的预警还非常困难。这是因为这些稳定性评价指标的完备性、科学性和灵敏性很难保证,特别是警限的确定非常棘手。通过稳定性评价指标对区域水资源可持续利用预警成功的基础是对稳定性评价指标理论的深入分析和实践的广泛运用,然而目前区域水资源系统稳定性的理论分析还没有得到重视,实践应用还没有展开。因此我们的区域水资源稳定性的预警分析与可持续性的预警分析采取了不同的策略即由指标预警转向模型预警。

3.4.2.3　稳定性的模型预警法

模型预警法是预警系统的基本方式之一,这种预警方法不必引入先行指标,而只考察警素指标时间序列的变动规律,通过建立警素指标的数学模型直接给出预警的判据。

区域水资源系统的不稳定性是系统无序化的表现即熵污染的结果。“熵”来源于希腊字“Entrepein”,原义为交换。1850年,克劳修斯 (K.Clausium)提出热力学第二定律:在一个孤立系统中,能量总是从温度高的物体流向温度低的物体,最后达到平衡。它可以用“熵”来度量,又称“熵增加定律”。熵是系统无序程度的量度,是系统不可逆性和均匀性的量度。根据热力学第二定律,自然界总是向混乱无序的方向发展,但实现却恰恰相反,自然界的物质进化和人类社会的进化,都一直朝着有序化的方向发展。为此,1994年薛定谔引进了“负熵”的概念。负熵是系统组分有序组合程度的一种度量。在信息中,熵的确是描述不确定性大小的量度,熵越大不确定性越大。

区域水资源系统是一个熵变系统,因此在其稳定性的预警分析中,我们引进熵模型。随着区域社会经济技术的迅速发展,人们对区域资源需求的量和质进一步膨胀和提高,水资源开放表现出来的资源系统在时间序列上的变化日益明显。这种变化过程既有热力学第二定律所描述的封闭系统熵增加的特点,也有开放系统接受太阳能负熵不断贮存的趋势。区域水资源系统的熵变化模型可以用下述代数式表示:

d S=diS+deS,其中:d S 是系统内的总熵,deS 是外部环境进行物质和能量交换引起的熵流,diS 是系统内部的不可逆过程引起的熵产生。

区域水资源系统是一个非平衡的、非线性的开放系统,如果deS＜-diS,则总熵d S小于0,可见负熵流可以使系统的熵减少。由于熵并非守恒量,区域水资源系统的总熵随时间的变化可以表述为:

式中:Js为通过单位面积的熵的交换率,即熵流；σ为单位体积产生的速率,即熵产生。

则有:

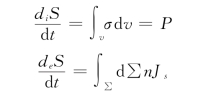
如果用Jk表示和速率有关的k 种不可逆过程的广义流 (Generalized Flux),Xk表示和推动力有关的第k 种不可逆过程的广义力(Generalized Force),则熵产生可以表达为:

当系统内部自激的不稳定因素和环境施加的干扰因素迫使区域水资源离开平衡态时,宏观不可逆过程随即开始,于是广义力和广义流都不等于零。广义力是产生广义流的原因,因此可以认为广义流是广义力的某种函数。假定这种函数关系存在且连续,并可以以平衡态即力和流皆为零时作为参考态作Taylor展开:

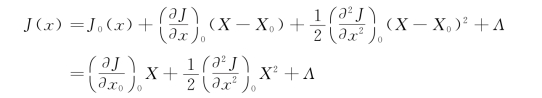
当广义力很弱,系统偏离平衡态很小,则力的高次幂可以忽略,则

满足这种线性关系的非平衡态称为非平衡态的线性区。如果广义不是很弱时,J(x)的展开式中包含有力的高次项,广义流就是广义力的非线性函数,这时的非平衡态称为非平衡态的非线性区。此时将熵S 和P 在稳定态附近展开并经过严密推导可得如下关系:

区域水资源系统是一个非平衡的、非线性的开放系统,因此区域水资源系统稳定性的预警分析的关键是确定广义力和广义流相对于稳定态的扰动所引起的超熵变化,也就是对δxp=0 的判断即所谓的警限确定。

区域可持续发展机制研究的成果表明,如果用E(t)表示系统的发展过程,这个过程可以使用Logistic模型来近似刻画:

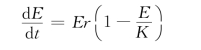
式中:r为内禀增长率；K 为环境容量；E 为发展要素。

1838年Verhulst提出的Logistic模型,被人们广泛地使用,不仅在自然科学,在社会科学中也是如此。Deevey认为这种增长型可能是最普遍的。Logistic模型在区域可持续发展机制研究中的应用是基于这样的认识,需求是发展的动力,资源环境的有限性是发展的阻力,可持续发展的实质是协调两者的关系,以一定的发展速度发展的同时,不危害资源环境的承载力,其目的是保持发展。尽管Logistic模型还存在很多问题,但是在还没有更好的模型描述的前提下,也不失为一种明智的选择。

用Logistic模型描述区域水资源系统的可持续发展过程,有必要对其参数作一诠释。E 为区域水资源系统的某一发展要素,如蓄水量、供水量等；r 为内禀增长率是发展要素在最有利条件下所能达到的最大增长率即增长潜力 (Developing Potential)；K 为环境容量,区域水资源的发展必然要受到区域的自然-经济-社会合系统的环境容量的限制,所谓的环境容量就是区域水资源系统外部环境提供给水资源发展的生产潜力和给予的发展限制即承载力(Carrying Capacity)。

为了获取区域水资源系统稳定性的警限,我们对Logistic模型进行分析,它的广义流为:

这个系统的非平衡态的线性区,熵产生是:

为了进一步明确Logistic模型的数学含义,我们对Logistic模型进行稳定性的数理解析:

对Logistic模型的发展曲线求二阶导数可得:

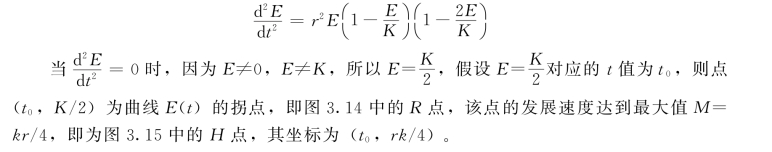
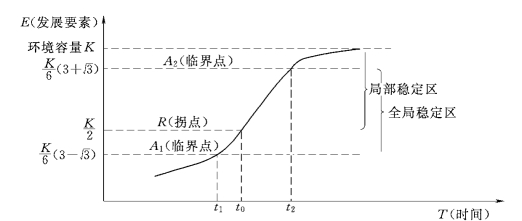
图3.14　E(t) 发展过程曲线

对Logistic型的发展曲线求三阶导数可得:

图3.15　d E/d t发展速度曲线