1.惯量匹配

进给系统对动态性能的要求主要包括加减速快、响应平稳、抗扰动能力强、稳定性好四方面，伺服电动机的加减速能力、机械传动系统的刚度和死区是影响系统动态响应性能的主要因素。真正意义上的进给系统动态设计，需要通过建立系统数学模型、确定系统传递函数或状态方程、构建系统结构框图等步骤，利用经典控制理论或现代控制理论进行，其分析与计算极为复杂，且由于系统非线性因素的影响，其准确性也有一定的局限。因此，在工程设计时，通常只需要进行电动机惯量匹配、加减速能力的计算，系统的动态调整与优化直接通过伺服调试软件自动完成。

理论和实践证明：当进给传动系统的结构设计合理时，对于电动机和丝杠直连、同步带连接或采用1～2级齿轮减速的系统，为了保证系统具有良好的动态性能，其惯量匹配原则和加减速能力要求如下。

式中J_L——负载惯量（kg·m²）；

J_M——电动机转子惯量（kg·m²）；

M_B——加减速转矩（N·m）；

M_S——电动机静态转矩（N·m）。

2.加减速要求

旋转运动系统的转矩平衡方程如下：

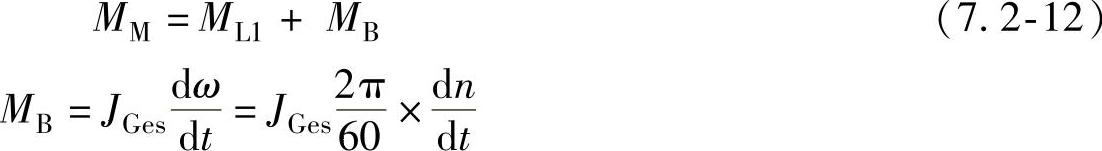
如果系统采用线性加减速，其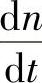恒定，假设从0加速到最大转速n_m的时间为t_H，则有：

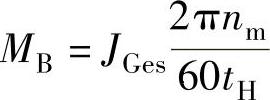
因此，如电动机加速转矩M_B为已知，则其加速时间t_H可通过下式计算：

以上计算式中各参数的含义如下：

J_Ges——系统总惯量（kg·m²）；

M_M——电动机输出转矩（N·m）；

M_L1——负载转矩（N·m），包括摩擦转矩ΣM_R与重力转矩M_G；

M_B——电动机加减速转矩（N·m）；

ω——电动机角速度（rad/s），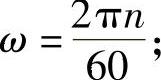

n——电动机转速（r/min）。

机床进给系统的加减速性能以最大加速度a_m和快进速度v_m指标衡量。对于加速度为a_m的线性加减速，从0加速到快进速度v_m的加速时间t_a为

式7.2-14中的快进速度v_m指标可根据电动机最高转速、机械传动系统结构计算得到，表7.2-3为国外推荐的不同数控机床的加速度a_m的参考值。

表7.2-3 数控机床推荐的加速度值

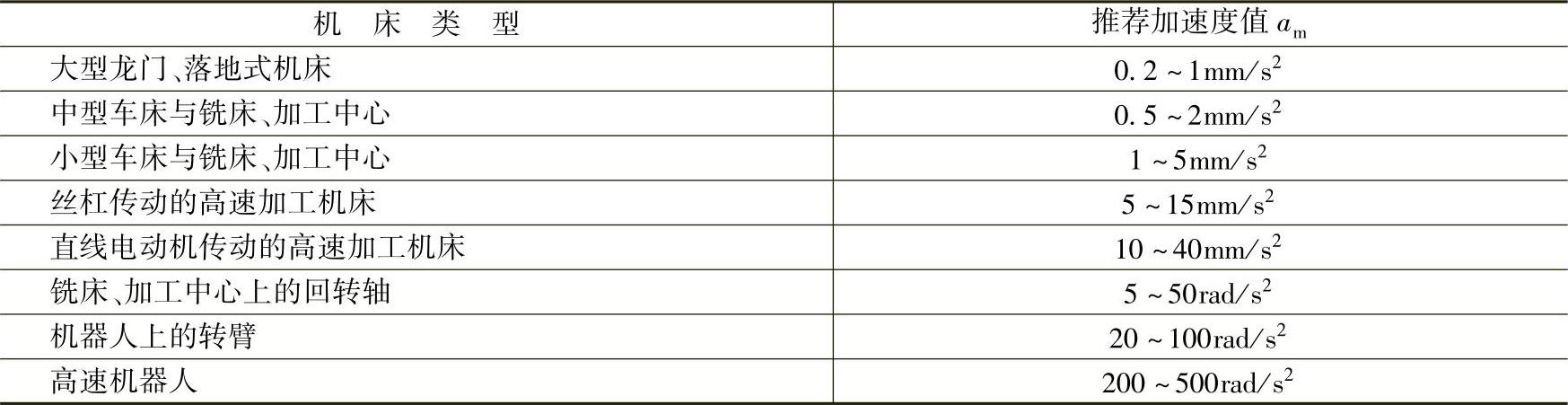
表7.2-3的推荐数据为数控机床的一般要求，在实际设计时，即使对于同一机床的不同坐标轴，有时也需要使用不同的加速度。例如，立式机床的垂直轴Z、卧式机床的垂直轴Y，由于重力作用，其加速度一般略低于其他轴。

式7.2-13计算得到的加速时间t_H是进给系统实际可以达到的加速时间，而式7.2-14计算得到的加速时间t_a则是机床设计要求的加速时间，因此，需要保证：

t_H≤t_a （7.2-15）

3.惯量计算

计算系统实际加减时间，需要确定系统惯量J_Ges。在滚珠丝杠传动系统中，系统惯量包括旋转运动部件惯量及直线运动部件折算到电动机的惯量两大部分。旋转运动部件惯量主要包括电动机转子惯量J_M、滚珠丝杠惯量J_SP、联轴器（或齿轮、同步带轮）惯量等；直线运动部件有工作台、拖板、工件等。惯量的计算方法如下。

1）旋转运动部件。旋转运动部件中的电动机转子惯量J_M可直接从电动机样本中查得；滚珠丝杠、联轴器、齿轮、同步带轮等部件的惯量。可按照如下实心圆柱体的惯量计算式，通过加减运算合成。

式中J_C——实心圆柱体惯量（kg·m²）。

γ——材料密度（kg/m³）。

D——实心圆柱体直径（m）。

L——实心圆柱体长度（m）。

对于钢制零件，代入密度、并折算为常用单位后，计算式可简化为：

J_C=0.77×10^-12d⁴l （7.2-17）

d和l分别为实心圆柱体直径和长度（mm）。(www.daowen.com)

2）直线运动部件。直线运动的工作台、拖板、工件等部件的惯量计算公式为

式中J_Z——直线运动部件惯量（kg·m²）；

m——运动部件重量（kg）；

h_sp——丝杠导程（m）；

4.计算实例

【例6】 对于例4、例5的立式加工中心，如X、Y轴的驱动电动机选择βiS12/3000，Z轴驱动电动机选择βiS22/2000，机床要求的X/Y轴加速度为5m/s²；Z轴加速度为4m/s²，进给系统的加减速能力可计算如下。

X轴：直线运动部件的惯量：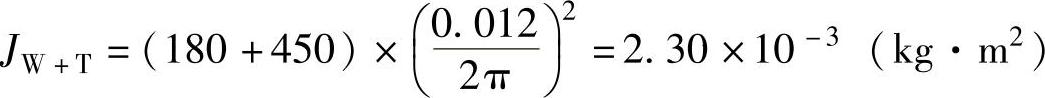

滚珠丝杠的惯量：J_sp=0.77×10^-12×40⁴×1000=1.97×10^-3（kg·m²）

联轴器等件的惯量：J_Gt=0.3×10^-3（kg·m²）

负载总惯量：J_L=4.57×10^-3（kg·m²）

βiS12/3000电动机转子惯量：J_M=2.28×10^-3（kg·m²）

系统总惯量J_Ges=6.85×10^-3（kg·m²）

从电动机加减速曲线可查得，βiS12/3000在转速n_m=2667r/min时的短时输出转矩M_M为22N·m，根据例2的计算结果有：

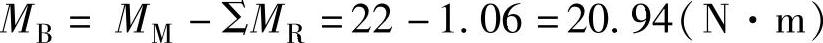
因此，X轴实际可达到的加速时间为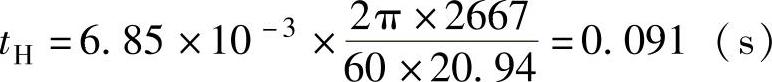

而机床设计要求的加减速能力为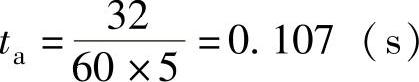故可满足式（7.2-11）及式（7.2-15）的要求。

Y轴：

直线运动部件的惯量：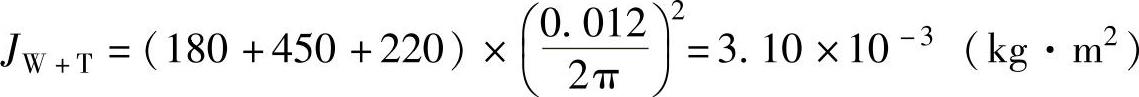

滚珠丝杠的惯量：J_sp=0.77×10^-12×40⁴×800=1.58×10^-3（kg·m²）

联轴器等件的惯量：J_Gt=0.3×10^-3（kg·m²）

负载总惯量为：J_L=4.98×10^-3（kg·m²）

βiS12/3000电动机转子惯量：J_M=2.28×10^-3（kg·m²）

系统总惯量J_Ges=7.26×10^-3（kg·m²）

根据例2的计算结果有：M_B=M_M-ΣM_R=22-1.16=19.84（N·m）

Y轴实际可达到的加速时间为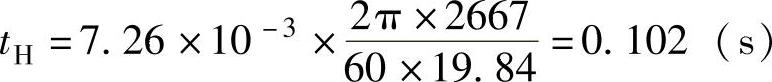

机床设计要求的加减速能力与X轴同，故同样可满足式（7.2-11）及式（7.2-15）的要求。

Z轴：直线运动部件的惯量：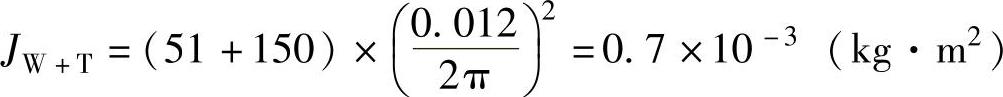

滚珠丝杠的惯量：J_sp=0.77×10^-12×40⁴×900=1.77×10^-3（kg·m²）

联轴器等件的惯量：J_Gt=0.3×10^-3（kg·m²）

负载总惯量为：J_L=2.77×10^-3（kg·m²）

βiS22/2000电动机转子惯量：J_M=5.87×10^-3（kg·m²）

系统总惯量J_Ges=8.64×10^-3（kg·m²）

从电动机加减速曲线可查得，βiS22/2000在转速n_m=2000r/min时的短时输出转矩M_M为27N·m，根据例2的计算结果有：

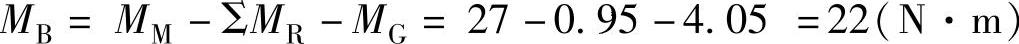
Z轴实际可达到的加速时间为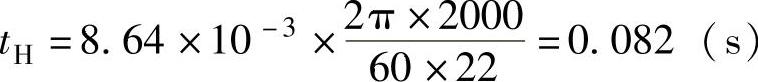

机床设计要求的加减速能力为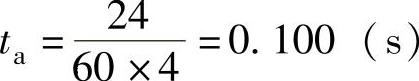

同样可满足式（7.2-11）及式（7.2-15）的要求。

以上为线性加减速的数控机床进给系统加减速能力校验的基本方法，但是，高速、高精度机床一般采用加速度变化率恒定的S形加减速，其计算方法与线性加减速不同，有关内容可参见本书作者编写、机械工业出版社出版的《FANUC-0iD选型与设计》一书。