（1）均匀分布

设随机变量X的密度函数为

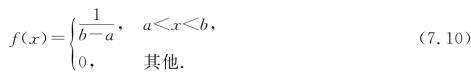
则称X在区间（a，b）上服从均匀分布，其中a，b为参数，记作X～U（a，b）.

均匀分别的密度函数图形如图7-5.

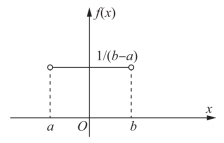
图7-5

均匀分布在实际中有广泛的应用，如第6章的几何概型中涉及的随机变量都服从均匀分布；乘客的候车时间X；在某个区间随机取一个数X等.

[例7.9]　设区间（0，5）中任意取一个数X，求一元二次方程4x2+4Xx+X+2=0有实根的概率.

解　设“一元二次方程4x2+4Xx+X+2=0有实根”事件为A；因X～U（0，5），而“方程4x2+4Xx+X+2=0有实根”事件等于“（Δ=（4X）2-4×4×（X+2）≥0）”事件.故所求概率为

（2）指数分布

设随机变量X的密度函数为

其中λ＞0是常数，则称X服从参数为λ的指数分布，记作X～E（λ）.

指数分布的密度函数图形分别如图7-6.

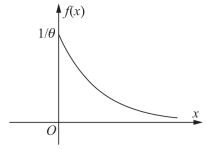
图7-6

指数分布有很广泛的应用，如电子元件的寿命，保险丝的寿命，随机服务系统中的服务时间，系统的可靠性等.

[例7.10]　某个系统有5个独立工作的同类型电子元件，每个元件的寿命X服从参数为的指数分布；求该系统在最初使用的200小时内至少有1只电子元件损坏的概率.

解　设一只电子元件寿命超过200小时的概率为p，则

令Y表示5个电子元件中损坏的个数，显然有Y～B（5，1-p），故所求概率为

指数分布的有趣的特性：

对任意s，t＞0，有

称为指数分布的无记忆性.

事实上

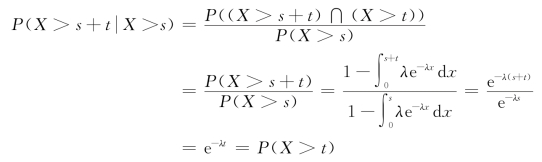
式（7.12）表明：如果X表示的是某元件的使用寿命，那么在元件已经使用了s小时的条件下还能使用t小时（即该元件总共使用了s+t小时）的概率，等于此元件从开始到至少使用t小时的概率.通俗地说就是元件对已使用过s小时是没有记忆的，这也是指数分布广泛应用的重要原因.

（3）正态分布

设随机变量X的密度函数为

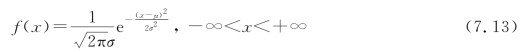
其中μ，σ（σ＞0）是常数，则称X服从参数为μ，σ2的正态分布或高斯分布，记作X～N（μ，σ2）.正态分布的密度函数图形如图7-7.

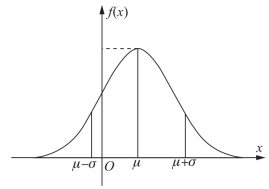
图7-7

正态分布的密度函数曲线有如下特性：

（1）关于x=μ对称，并在x=μ处取得最大值

（2）在x=μ±σ处有拐点，x轴是其渐近线；

（3）固定σ，改变μ值，曲线沿x轴方向左右平移，但形状不变，可见μ为位置参数（如图7-8）；固定μ，σ值越大，曲线越平坦，σ值越小，曲线越陡峭，因此σ为形状参数（如图7-9）.

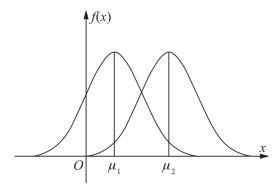
图7-8(www.daowen.com)

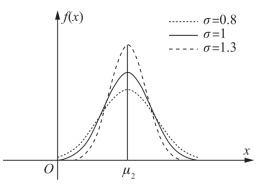
图7-9

在自然及社会现象中，大量的随机现象都服从正态分布，因而正态分布在概率论中有非常特殊的地位.如测量误差，袋装物体的重量，人的身高、体重等都服从正态分布.一般地，如果一个随机变量受到众多微小独立的随机因素的影响，那么该随机变量近似服从正态分布.

当X～N（μ，σ2）时，其中μ=0，σ=1时，则称X服从标准正态分布，记作X～N（0，1）.它的密度函数和分布函数分别用专用符号φ（x）和Φ（x）表示，即

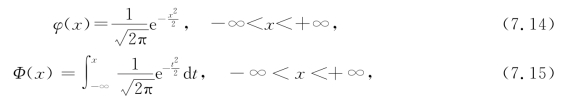
它们的图像分别如图7-10和图7-11.

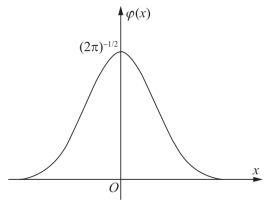
图7-10

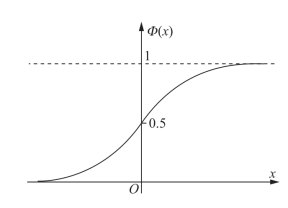
图7-11

由对称性可得标准正态分布的性质：

性质7.6

Φ（-x）=1-Φ（x），　-∞＜x＜+∞.　（7.16）

对随机变量服从标准正态分布时概率的计算，专家已专门编制了Φ（x）的函数值表（见附表一），供查用.

[例7.11]　设X～N（0，1），求

(1)P(1＜X＜3);(2)P(|X|＜1);(3)P(|X|＞2);(4)P(|X|＞-1);

解　利用性质及查附表

(1)P(1＜X＜3)=Φ(3)-Φ(1)=0.9987-0.8413=0.1574

(2)P(|X|＜1)=P(-1＜X＜1)=Φ(1)-Φ(-1)=Φ(1)-(1-Φ(1))

=2Φ(1)-1=2×0.8413-1=0.6826

(3)P(|X|＞2)=1-P(-2＜X＜2)=2(1-Φ(2))=2(1-0.9772)=0.0456

(4)

随机变量服从非标准正态分布时概率的计算可以通过线性变换转化为标准正态分布，再求得.

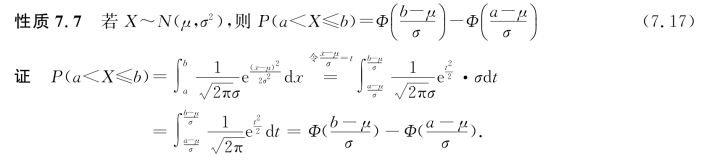
[例7.12]　设X～N（3，4），求

(1)P(2≤X＜5);　(2)P(X≥4.3);

（3）确定常数c，使得P（X＜c）=0.6554；

（4）确定常数d，使得P（X＜d）=P（X＞d）

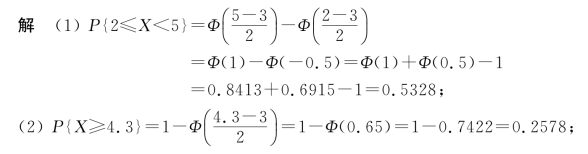
（3）因为P（X＜c）=0.6554，查附表得c=0.4；

（4）P（X＜d）=P（X＞d）=1-P（X＜d），即

P(X＜d)=0.5

由非标准正态分布的对称轴特征有d=3.

[例7.13]　某城市的公共汽车车门的高度是按该市成年男性乘车时碰头机会不超过1%来设计的，假设成年男性身高X～N（170，62）（单位为mm），问车门高度h设定多高才合理.

解　由已知得

P（X＞h）≤0.01，即P（X≤h）≥0.99

由（7.17）得

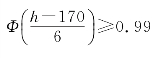
查附表一可得

由分布函数的不减性可得

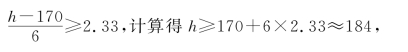
因此车门高度h定为184mm才合理.