仔细观察已知离散型随机变量的分布律求它的分布函数F(x)=P(X≤x)时,只是把满足(X≤x)取值的所有概率值相加,那么如果在连续型随机变量的分布函数已知时,也可以看成把满足(X≤x)取值的所有概率值(只是趋于0)相加,而这正好契合了微积分中的积分的概念.例如在例7.2中,随机变量X的分布函数为
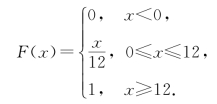
记
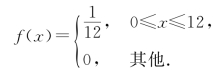
这是一个类似离散型随机变量分布律的函数,F(x)可表示为f(x)的在区间(-∞,x)上的积分,即
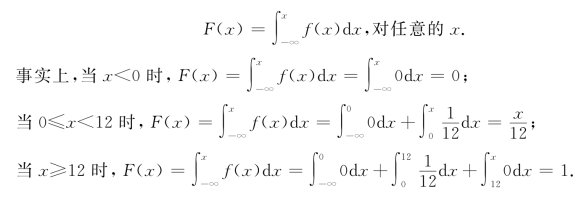
归纳就有下列定义.
定义7.4 如果随机变量X的分布函数F(x)总存在非负可积函数f(x),使得对任意的实数x,有
![]()
成立,则称X为连续型随机变量,称f(x)为X的概率密度函数,简称密度函数.
连续型随机变量的密度函数f(x)有下以性质:
性质7.1 f(x)≥0.
性质7.2 ![]()
性质7.3 对任意a,b∈R,有
![]()
由以上的性质可知:概率密度函数曲线总位于x轴上方;介于它和x轴之间的面积等于1,如图7-3;随机变量落在区间(a,b]的概率P{a<X≤b}等于区间(a,b]上曲线y=f(x)与x轴所围成的曲边梯形的面积,如图7-4.
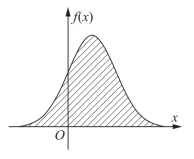
图7-3
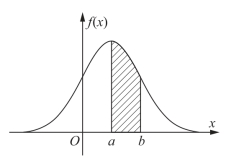
图7-4
性质7.4 对任意的实数a,P{X=a}=0.
证 对任意Δx>0,有
![]()
令Δx→0,由夹逼定理可得P{X=a}=0.(https://www.daowen.com)
此性质表明:不可能事件的概率必为0,但概率等于零的事件可以不是不可能事件;同样地,必然事件的概率必为1,但概率等于1的事件可以不是必然事件.
性质7.5 F′(x)=f(x).
此性质给出了连续型随机变量的分布函数与密度函数之间的关系:分布函数的导数是概率密度函数,反之,概率密度函数的积分函数是分布函数,如式(7.9).
[例7.7] 设随机变量X的密度函数为
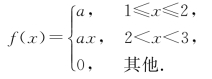
其中a>0,试求:(1)常数a;(2)P{-1<X≤2.5};(3)X的分布函数F(x).
解 (1)由密度函数的性质![]() 有
有
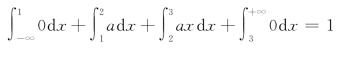
计算得![]()
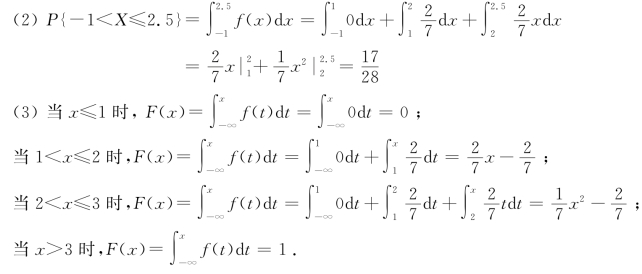
综合得X的分布函数F(x)为
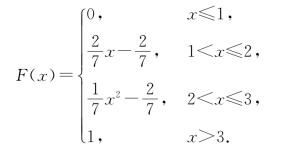
[例7.8] 设连续型随机变量X的分布函数为
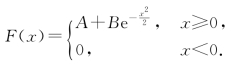
试求(1)常数A和B;(2)P{X≤2};(3)X的概率密度函数.
解 由连续型随机变量分布函数性质得
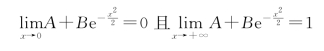
即
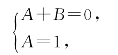
解得
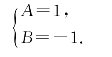
(2)P{X≤2}=F(2)=1-e-2.
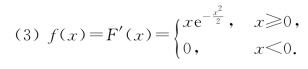
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







