(1)两点分布
如果随机变量X的分布律为
P{X=k}=pk(1-p)1-k,k=0,1, (7.3)
其中0<p<1,则称随机变量X服从两点分布或者(0-1)分布.也可以用表格的形式表示:
两点分布是一种简单又常用的分布.例如在质量检验中,产品质量是否合格可以用两点分布来描述,动物的性别,医用检测的阴性阳性等;但凡随机试验的结果只有2个分布,都服从两点分布.
(2)二项分布
如果随机变量X的分布律为
其中0<p<1,则称X服从参数为n和p的二项分布,记为X~B(n,p),如下表.
特别地,当n=1时,二项分布B(1,p)就是两点分布.
二项分布是一个非常重要的分布,实际中的许多随机现象都服从二项分布.如果随机试验是n重伯努利试验,即每次试验的结果只有2个,即事件A发生或A不发生,关注的随机变量X是A发生的次数,则X一定服从B(n,p).
[例7.4] 已知某保险公司的一人寿险种有1000人投保,由以往数据可知他们一年中意外死亡的概率为0.005,且相互间独立.试求在未来的一年里这1000人中死亡人数不超过10人的概率.
解 设随机变量X是在未来的一年里这1000人中死亡的人数,1000人的投保可看成同一人投保1000次,所以X~B(1000,0.005).则在未来的一年里这1000人中死亡人数不超过10人的概率为
(3)泊松分布
如果随机变量X的概率分布为
其中λ>0是常数,则称X服从参数为λ的泊松分布,记为X~P(λ)或X~π(λ).
定理7.1(泊松定理) 设λ>0是常数,n为任意正整数,且满足npn=λ,则对任意固定的非负整数k,有
证明略.
这一结论告诉我们,当n很大,而p很小时可以将二项分布的计算转化为泊松分布来近似计算,即
在实际应用中也有大量随机现象会服从泊松分布.例如一本书中的印刷错误数;某地区一个月内快递丢失的数量;医院在一天内到来的急诊的人数;火车站候车室的乘客人数;放射性物质在某单位时间内放射的粒子数等.
[例7.5] 某商店中出售一商品,根据历史记录分析,每月销售量服从泊松分布,参数为7,问在月初进货时要库存多少件此种商品,才能以0.99的概率充分满足顾客的需求.(www.daowen.com)
解 设商店每月销售此种商品X,月初的进货量为x件,由假设可知当X≤x时就能充分满足顾客的需求,故有
P(X≤x)≥0.99
因为X~P(7),上式等价于
通过试根可得
因此这家商店只要在月初进货时保证库存不少于14件,就能以0.99的概率充分满足顾客的需求.
(4)几何分布
如果随机变量X的概率分布为
P(X=k)=(1-p)k-1p, k=1,2… (7.7)
其中0<p<1,则称X服从参数为p的几何分布,记为X~G(p).
如随机试验E只有两个可能的结果A与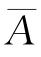 ,记A发生的概率为p,则将实验独立重复进行下去,直到事件A发生为止,如果用X表示所需进行试验的总次数,则X是一个随机变量并服从几何分布(俗称首次成功模型).
,记A发生的概率为p,则将实验独立重复进行下去,直到事件A发生为止,如果用X表示所需进行试验的总次数,则X是一个随机变量并服从几何分布(俗称首次成功模型).
[例7.6] 某市发行某种彩票,每张1元,中奖率为0.0001;某人每次购买1张彩票,如果不中奖则再继续购买1张,直到中奖为止.试求该人购买多少次才以98%的概率保证中奖.
解 设随机变量X表示该人购买的次数,则易判断X服从几何分布,p=0.0001;假设该人购买n次才以98%的概率保证中奖,则有
P(X≤n)=0.0001+0.0001×(1-0.0001)+…+0.0001×(1-0.0001)n-1≥0.98
解得n≥39119,即该人购买39119次才以98%的概率保证中奖.
(5)超几何分布
如果随机变量X的概率分布是
则称X服从超几何分布.
这实际就是从含有M件次品的总共N件产品中任取n件产品,随机变量X表示n件产品里恰好包含的次品数,那么n件产品里恰好包含的次品数为k件的概率为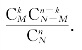
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






