定义7.2　设X是一随机变量，对任意的实数x，函数

F(x)=P(X≤x)　(7.1)

称为随机变量X的分布函数.

[例7.1]　一盒中装有6张卡片，分别有3张、2张、1张写有数字-1，0，5；现从盒子任取1张卡片，随机变量X表示取得的卡片上的数字，求X的分布函数.

解　易得随机变量X可能取值为-1，0，5，取值的概率分别为则

当x＜-1时，（X≤x）是不可能事件，所以F（x）=0；

当-1≤x＜0时，（X≤x）与（X=-1）是相等事件，所以

当0≤x＜5时，（X≤x）与（X=-1）∪（X=0）是相等事件，所以

当x≥5时，（X≤x）是必然事件，所以F（x）=1.

综合可得

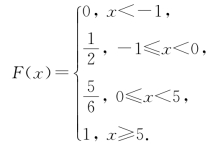
分布函数的图形见图7-1.

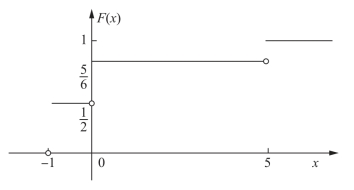
图7-1

[例7.2]　一陀螺的周边标有刻度[0，12），旋转陀螺直至其停下，随机变量X表示陀螺停下时与桌面相切的切点的刻度，求X的分布函数.(www.daowen.com)

解　易得随机变量X可能取值为任意实数，但只有在[0，12）取值是有意义的，且理论上X取[0，12）中的某一确定值的概率是趋于0的.则

当x＜0时，（X≤x）是不可能事件，所以F（x）=0；

当0≤x＜12时，（X≤x）与（0≤X≤x）是相等事件，而X取值的概率与区间的长度成正比，所以

当x≥12时，（X≤x）是必然事件，所以F（x）=1.

综合可得

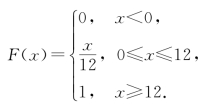
分布函数的图形见图7-2.

分布函数具有如下基本性质：

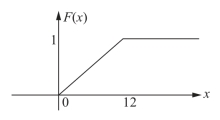
图7-2

(1)0≤F(x)≤1,-∞＜x＜+∞;

（2）若x1＜x2，则F（x1）≤F（x2）（单调不减）；

（3）及

（4）右连续性：对任意的实数

若某一函数具有上述性质，则它一定是某一随机变量的分布函数.