对同一随机试验的两个事件A，B，如果

则称事件A是独立于事件B的（或称事件B是独立于事件A的）.结合条件概率公式易得

P(AB)=P(A)P(B)　(6.18)

定义6.4　对于两事件A与B，如果

P(AB)=P(A)P(B)

成立，则称A与B相互独立，简称A与B独立.

[例6.28]　甲家庭中有若干个小孩，假定生男生女是等可能的，记A表示“家庭中男女孩都有”，B表示“家庭中最多有一个女孩”.试问以下两种情形下事件A与B是否独立？

（1）家庭中有两个小孩；　（2）家庭中有三个小孩.

解　（1）样本空间中含有4个样本点，且它们是等可能出现的.所以

于是P（AB）≠P（A）P（B）即事件A与B是不相互独立的.

（2）样本空间中含有23=8个样本点，且它们是等可能出现的，易得

所以有P（AB）=P（A）P（B），即事件A与B相互独立.

在实际问题中，人们往往从直观经验判断独立性，即：如果两个事件的发生与否彼此间没有影响，则认为这两个事件是相互独立的.

[例6.29]　甲、乙两射手独立地向同一目标射击一次，命中率分别为0.9和0.8，求目标被击中的概率.(www.daowen.com)

解　设A表示“甲击中目标”，B表示“乙击中目标”，C表示“目标被击中”，由经验可知A与B独立，且C=A∪B.已知P（A）=0.9，P（B）=0.8，于是所求概率

P(C)=P(A∪B)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(A)P(B)

=0.9+0.8-0.9×0.8=0.98

定理6.3　下列四组事件：A与B；与B；A与相互独立是等价的.

证明　只证A与B独立和A与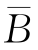独立是等价的.

如A与B独立，由概率的性质知

因A与B独立，即

P(AB)=P(A)P(B).

所以有

即A与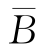独立.

反之，如A与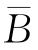独立，即

特别注意，一般情形下两事件间的独立性与两事件的互不相容没有关联，千万不要混淆，因为事件A与事件B互不相容（P（A）＞0，P（B）＞0），即AB=∅，则有P（AB）=0，但P（AB）≠P（A）P（B）＞0，也即A与B是不相互独立的.