根据概率公理易得如下性质.利用概率的这些性质，可以计算复杂事件的概率.

性质1

P（∅）=0.　（6.4）

性质2　（有限可加性）若A1，A2，…，An是一组两两互不相容的事件，则

性质3

P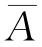（）=1-P（A）.　（6.6）

性质4

P（B-A）=P（B）-P（AB）.　（6.7）

特别，如A⊂B，则P（B-A）=P（B）-P（A）.

性质5

P（A∪B）=P（A）+P（B）-P（AB）.　（6.8）(www.daowen.com)

推广有

P(A∪B∪C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC).　(6.9)

[例6.17]　已知P（A）=0.6，P（A∪B）=0.8，P（AB）=0.2，求P（B）.

解　由P（A∪B）=P（A）+P（B）-P（AB）得

P(B)=P(A∪B)-P(A)+P(AB)=0.8-0.6+0.2=0.4.

[例6.18]　设P（A）=P（B）=P（C）=0.25，P（AB）=0，P（AC）=P（BC）=，求A，B，C都不发生的概率.

解　A，B，C都不发生，即，故

[例6.19]　据资料，某市居民私房拥有率87%，私车拥有率45%，无房无车的占23%，求任意抽查一户居民恰为有房有车的概率.

解　A表示“居民有私房”，B表示“居民有私车”，则所求即为P（AB）.已知P（A）=0.87，P（B）=0.45，，则