概率论发展初期，确定概率的常用方法诸如：掷一颗完全均匀的骰子，出现每一个点数的可能性都是.这样的随机试验具有如下两个特点：

（1）试验的所有结果只有有限个；　（2）试验的基本结果出现的可能性相同.

具有上述两个特点的随机试验称为古典概型的随机试验，简称为古典概型.

定义6.1　在古典概型中，设随机试验的样本空间Ω由n个样本点构成，A为任意一个事件且含有nA个样本点，则事件A发生的概率

此概率称为古典概率.

显然，满足古典概型的事件A的概率计算的方法可归结为：计算样本空间Ω中的样本点个数和事件A中含有的样本点个数；因此加法原理、乘法原理、排列、组合等计数的工具是必需的.

[例6.11]　抛掷一颗均匀的骰子两次，求下列事件的概率.

（1）两次点数之和为5；　（2）两次点数相同；

（3）两次点数差为2；　（4）至少有一次得到4点.

解　抛一颗均匀的骰子两次，记第一、二次出现的点数分别为i、j，则试验的样本空间Ω={（i，j）|i，j=1，…，6}，样本空间Ω中的样本点总数n=6×6=36，且各样本点出现是等可能的，这是古典概型问题.

（1）设A=“两次点数之和为5”，则A中包含的样本点数为nA=4，所以事件A发生的概率为(www.daowen.com)

（2）设B=“两次点数相同”，则B中包含的样本点数为nB=6，所以事件B发生的概率为

（3）设C=“两次点数差为2”，则C中包含的样本点数为nC=8，所以事件C发生的概率为

（4）设D=“至少有一次得4点”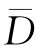，=“没有一次得4点”，其包含的样本点数为，所以事件D发生的概率为

[例6.12]　（无放回摸球模型）一口袋中有M个白球，N-M个黑球，从中无放回任取n个，求此n个球中恰有m个白球的概率.

解　设事件A表示“n个球中恰有m个白球”，样本点总数为事件A的概率为

[例6.13]　（有放回摸球模型）一口袋中有M个白球，N-M个黑球，从中有放回任取n个，求此n个球中恰有m个白球的概率.

解　设事件A表示“n个球中恰有m个白球”.因是有放回抽样的方式，可得样本空间有Nn个样本点；事件A有样本点数为故事件A发生的概率

[例6.14]　求10个人中至少有两人生日相同的概率.

解　设A=“10个人中至少有两人生日相同”，则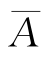=“10个人的生日全不相同”.所以