（1）包含关系（子事件）

若A事件发生必然导致B事件发生，则称B事件包含A事件，也可称A是B的子事件，记作A⊂B（图6-2）.

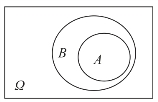
图6-2

例如在抛骰子试验中，记事件A=“出现的点数是2点”，B=“出现偶数点”；则A发生（出现2点）必然导致事件B（2点是偶数点）的发生，故A⊂B.

如果A与B事件互相包含，则称事件A与B相等，记为A=B.

例如在抛骰子试验中，记事件C=“出现的点数是4，5，6点”，D=“出现的点数大于3点”；则C事件与D事件相等，即C=D.

（2）和事件（并事件）

A事件或B事件的发生都导致该事件发生，此事件称为A事件与B事件的和（并）事件，记为A∪B（图6-3），即A事件与B事件至少有一个发生.

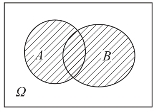
图6-3

n个事件A1，A2，…，An的和（并）事件可记为，表示“事件A1，A2，…，An中至少有一个发生”.而一系列事件A1，A2，…，An…的和（并）事件记为，表示“事件A1，A2，…，An，…中至少有一个发生”.

例如在抛骰子试验中，记事件A=“出现的点数是4，5，6点”，B=“出现的点数2，3，4点”；则A∪B=“出现的点数是2，3，4，5，6点”.

（3）积事件（交事件）

一事件发生必导致A事件与B事件都发生，该事件称为A事件与B事件的积事件或交事件，记为A∩B或AB（图6-4），即事件A与B同时发生.

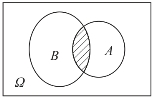
图6-4

n个事件A1，A2，…，An的积（交）事件可记为，表示“n个事件A1，A2，…，An同时发生”.

事件序列A1，A2，…，An，…的积事件可记为，表示事件A1，A2，…，An，…同时发生.

例如在抛骰子试验中，记事件A=“出现的点数是4，5，6点”，B=“出现的点数为1至4点”；则A∩B=“出现的点数是4点”.(www.daowen.com)

（4）互不相容事件

A事件与B事件不可能同时发生，称A事件与B事件为互不相容事件或互斥事件，记作AB=∅或A∩B=∅，如图6-5.

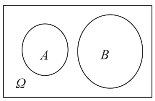
图6-5

若n个事件A1，A2，…，An中任意两个互不相容，则称n个事件A1，A2，…，An互不相容，如图6-6.

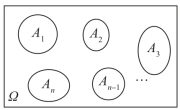
图6-6

例如在抛骰子试验中，记事件A=“出现的点数是4，5，6点”，B=“出现的点数1，2点”；则A∩B=∅，即A事件与B事件互斥.记Ai表示“出现点数是i点”，i=1，…，6，则A1，…，A6是一组互不相容事件.

（5）对立事件（逆事件）

A事件不发生这一事件称为A事件的对立事件，也称逆事件，记为，如图6-7.

显然有

图6-7

例如在抛骰子试验中，记事件A=“出现的点数是4，5，6点”，B=“出现的点数1，2，3点”；则A事件与B事件互逆，即

（6）差事件

A事件发生而B事件不发生的事件称为事件A对事件B的差事件，记为A-B，如图6-8（阴影部分）.例如在抛骰子试验中，记事件A=“出现的点数1，2，3，4点”，B=“出现的点数3，4，6点”，则A-B=“出现的点数1，2点”.

图6-8

显然有