下面我们用两个实例来说明如何利用配方法将二次型化为标准形.

1.含平方项的二次型的配方法

[例5.4]　利用配方法将二次型

化为标准形，并求出所作的可逆线性变换.

解　由于的系数不为零，先将所有含有x1的项配成一个完全平方，得

再将余下的所有含x2的项配成一个完全平方，得

令

即

由于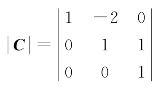=1≠0，则由x1，x2，x3到y1，y2，y3的可逆线性变换为

通过此变换可将二次型化为标准形

对于n元二次型f（x1，x2，…，xn），如果的系数不全为零，参照例5.4的方法可将其化为标准形；如果的系数全为零，此时可按下面例5.5的方法，将其化为标准形.

2.不含平方项的二次型的配方法(www.daowen.com)

[例5.5]　设二次型f（x1，x2，x3）=x1x2+x1x3-3x2x3，试用配方法将其化为标准形，并求出所作的可逆线性变换.

解　由于二次型中没有平方项，又x1x2的系数不为零，故先作一个可逆线性变换，将二次型化为含有平方项的形式，再用例5.4的方法解决.

令

简记为X=C1Y，其中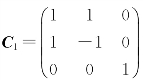为可逆矩阵，代入原二次型中，有

再参照例5.4中的配方法，先对含y1的项配完全平方，然后对余下的含y2的项配完全平方，得

令

即

简记为Y=C2Z，其中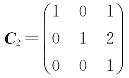为可逆矩阵.

由X=C1Y，Y=C2Z，得X=（C1C2）Z.记

从而有可逆线性变换X=CZ，即

通过此变换可将二次型化为标准形