定义5.1　含有n个变量x1，x2，…，xn的n元二次齐次多项式

称为x1，x2，…，xn的n元二次齐次多项式，简称为x1，x2，…，xn的n元二次型.

当aij（i，j=1，2，…，n）为实数时，f称为实二次型；当aij为复数时，f称为复二次型，本章仅讨论实二次型.

令aij=aji，i，j=1，2，…，n，则式（5.1）又可写成

进一步，有

利用矩阵乘法，式（5.2）可化为

若记

其中aij=aji（i，j=1，2，…，n），则二次型式（5.3）可以简洁表示为

f(x1,x2,…,xn)=XTAX,(www.daowen.com)

其中AT=A，称n阶实对称矩阵A为二次型f的矩阵，二次型f称为n阶实对称矩阵A的二次型，并称矩阵A的秩为该二次型的秩.

通过上述分析可以得到：n元实二次型与n阶实对称矩阵之间是一一对应的.

[例5.1]　求二次型的矩阵及其矩阵表示式，并求二次型的秩.

解　二次型f的矩阵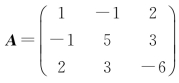，则二次型f的矩阵表示式为

因为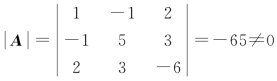，则矩阵A为可逆矩阵，所以R（A）=3，故二次型f（x1，x2，x3）=XTAX的秩等于3.

[例5.2]　二次型f的矩阵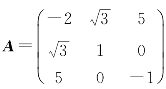，试写出矩阵A所对应的二次型f.

解　因为矩阵A为3阶实对称矩阵，故对应的二次型f是三元二次型，有