设n阶实对称矩阵A有m个互不相同的特征值λ1，λ2，…，λm，其中λi为A的ki重特征值（i=1，2，…，m），且k1+k2+…+km=n.由定理4.10知，A的对应于ki重特征值λi的线性无关的特征向量恰好有ki个.利用施密特正交化方法把这ki个线性无关的特征向量正交化，再单位化，可求得A的n个两两正交且单位化的特征向量组.把所得正交单位向量组组成矩阵U，则U是正交矩阵，且U-1AU为对角矩阵.

定理4.11　对于任意n阶实对称矩阵A，一定存在一个n阶正交矩阵U，使得U-1AU为对角矩阵.

由前面的讨论，得到对实对称矩阵A求正交矩阵U，使U-1AU为对角矩阵的方法.具体步骤如下：

（1）求出A的全部互异特征值λ1，λ2，…，λm.

（2）对A的每个ki重特征值λi（i=1，2，…，m），解特征方程组（λiE-A）X=0，求出它的一个基础解系ξi1，ξi2，…，ξiki，利用施密特正交化方法将ξi1，ξi2，…，ξiki先正交化，再单位化，得到A的对应于特征值λi的ki个正交单位化的特征向量ηi1，ηi2，…，ηiki.

（3）将对应于λi的全部特征向量ηi1，ηi2，…，ηiki（i=1，2，…，m）构成矩阵

U=(η11η12…η1k1η21η22…η2k2…ηm1ηm2…ηmkm),

即为所求之正交矩阵，且

[例4.11]　设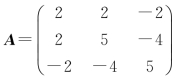，求正交矩阵U，使得U-1AU=Λ为对角矩阵.

解　A的特征多项式

得A的特征值λ1=λ2=1，λ3=10.(www.daowen.com)

当λ1=λ2=1时，解特征方程组（E-A）X=0，由于

得基础解系

正交化得

单位化得

当λ3=10时，解特征方程组（10E-A）X=0，由于

得基础解系

单位化得

令正交矩阵

有