定义4.8　设A是一个n阶实矩阵，如果ATA=AAT=E，则称A是正交矩阵.

由定义4.8可知，单位矩阵E为正交矩阵；不难验证在平面解析几何中两直角坐标系间的坐标变换矩阵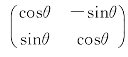也是正交矩阵.

正交矩阵具有如下性质.

定理4.6　设A、B都是n阶正交矩阵，则

(1)A-1=AT.

（3）AT（即A-1）是正交矩阵.

（4）AB是正交矩阵.

证　（1）因为A是n阶正交矩阵，则有ATA=AAT=E，所以A-1=AT.

（2）因为ATA=E，两边取行列式，得

因此，所以.

（3）因为AT（AT）T=（ATA）=E，且AT为实矩阵，所以AT（即A-1）也是正交矩阵.(www.daowen.com)

（4）因为A、B都是n阶正交矩阵，则有

(AB)(AB)T=(AB)(BTAT)=A(BBT)AT=AEAT=AAT=E,

又AB为实矩阵，所以AB也是正交矩阵.

定理4.7　n阶方阵A为正交矩阵的充分必要条件是A的列（或行）向量组是正交单位向量组.

证　将A按列分块为A=（α1α2…αn），有

易得ATA=E的充分必要条件是

即A的列向量组α1，α2，…，αn是正交单位向量组.

因为A是正交矩阵，由定理4.6得AT也是正交矩阵，所以AT的列向量组是正交单位向量组，即A的行向量组也是正交的单位向量组.

如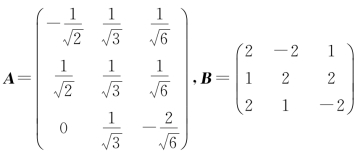，利用定理4.7容易验证A是正交矩阵，而B不是正交矩阵，因为B的行（或列）向量组虽然两两正交，但不是单位向量组.