定义4.6　如果两个n维实向量α与β的内积等于零，即（α，β）=0，则称向量α与β正交（或相互垂直），记为α⊥β.

由于零向量与任何向量的内积均为零，因此零向量与任意向量都正交.

定义4.7　如果n维非零实向量组α1，α2，…，αs两两正交，即

(αi,αj)=0,　(i≠j;i,j=1,2,…,s),

则称该向量组为正交向量组.

如n维单位向量组：，因为

(εi,εj)=0,　(i≠j;i,j=1,2,…,n),

所以ε1，ε2，…，εn是正交向量组.

由单位向量构成的正交向量组叫做正交单位向量组，也称标准正交向量组.

[例4.9]　已知三维向量α1=（0，1，1）T，α2=（1，1，-1）T，试求非零向量α3，使α1，α2，α3成为正交向量组.

解　因为（α1，α2）=0，所以α1与α2正交.现要求出α3，使α3与α1、α3与α2都正交即可.

设α3=（x1，x2，x3）T，由，得齐次线性方程组为

由

得基础解系ξ1=（2，-1，1）T，取α3=（2，-1，1）T即为所求.

定理4.4　正交向量组必定线性无关.

证　设α1，…，αi，…，αs是一正交向量组.设有一组数k1，…，ki，…，ks，使得

k1α1+…+kiαi+…+ksαs=0,　(4.13)

用αi与式（4.13）两边的向量作内积，得(www.daowen.com)

(αi,k1α1+…+kiαi+…+ksαs)=0,

即

k1(αi,α1)+…+ki(αi,αi)+…+ks(αi,αs)=0.

因α1，…，αi，…，αs是正交向量组，得

ki(αi,αi)=0.

由于αi≠0，则（αi，αi）＞0，所以ki=0.由于i（i=1，2，…，s）的任意性，便得α1，…，αi，…，αs线性无关.

注意：定理4.4的逆命题不成立.如线性无关，但α1，α2，α3不是正交向量组.

既然线性无关的向量组α1，α2，…，αs不一定是正交向量组，那么如何从线性无关的向量组α1，α2，…，αs中构造出与α1，α2，…，αs等价的标准正交向量组η1，η2，…，ηs呢？

定理4.5　设α1，α2，…，αs是线性无关的向量组，令

则β1，β2，…，βs是正交向量组.上述正交化过程称为施密特（Schimidt）正交化方法.

再将β1，β2，…，βs单位化，得

则向量组η1，η2，…，ηs是标准正交向量组，且向量组η1，η2，…，ηj与向量组α1，α2，…，αj（j=1，2，…，s）等价.

证　略.

[例4.10]　设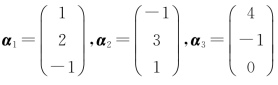，试用施密特正交化法将向量组正交化，再单位化.

解　取β1=α1，

再把β1，β2，β3单位化.因为，所以

则η1，η2，η3是与α1，α2，α3等价的正交单位向量组.