【摘要】:类似中学数学中两个向量的数量积的定义,我们可定义n维向量的内积.定义4.4设n维实向量,则称为向量α和β的内积,记作(α,β),即例如α=(1,-2,0,1)T,β=(2,0,1,3)T,则α和β的内积为(α,β)=1×2+(-2)×0+0×1+1×3=5.根据定义4.4和矩阵乘法,易得(α,β)=αTβ=βTα.设α,β,γ为n维实向量,易得向量内积具有下述性质:(1)(α,β)=(β,α).
类似中学数学中两个向量的数量积的定义,我们可定义n维向量的内积.
定义4.4 设n维实向量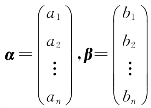 ,则
,则
称为向量α和β的内积,记作(α,β),即
例如α=(1,-2,0,1)T,β=(2,0,1,3)T,则α和β的内积为
(α,β)=1×2+(-2)×0+0×1+1×3=5.
根据定义4.4和矩阵乘法,易得(α,β)=αTβ=βTα.
设α,β,γ为n维实向量,易得向量内积具有下述性质:
(1)(α,β)=(β,α).
(2)(α+β,γ)=(α,γ)+(β,γ).
(3)(kα,β)=k(α,β),其中k为实数.
(4)(α,α)≥0,当且仅当α=0时,有(α,α)=0.
由于对任意向量α,有(α,α)≥0,因此可引入向量长度的概念.
定义4.5 对n维实向量α=(a1,a2,…,an)T,称(https://www.daowen.com)
为n维实向量α的长度(或模).
例如,向量α=(4,0,3)T的长度
向量的长度具有以下性质:
(1)‖α‖≥0,当且仅当α=0时,有‖α‖=0.
(2)‖kα‖=![]() ,其中k为实数.
,其中k为实数.
(3)‖α+β‖≤‖α‖+‖β‖.
(4)对任意两个n维实向量α,β,恒有
等号成立当且仅当α,β线性相关.
式(4.12)又称柯西不等式,它说明了任意两个n维实向量的内积与它们长度之间的关系.
长度为1的向量称为单位向量.对于任意n维非零向量α,向量![]() 显然是一个单位向量.事实上
显然是一个单位向量.事实上
用非零向量α的长度除非零向量α,得到一个单位向量的过程,称为将向量α单位化.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章





