对n阶方阵A,若存在可逆矩阵P,使P-1AP等于对角矩阵Λ,则称方阵A可以相似对角化,这个过程称之为把方阵A相似对角化.
定理4.1 n阶方阵A能与n阶对角矩阵Λ相似的充分必要条件是A有n个线性无关的特征向量.
证 先证必要性.设n阶方阵A能与n阶对角矩阵Λ相似,其中
则存在可逆矩阵P,使得P-1AP=Λ,即
AP=PΛ. (4.10)
把P按列分块,设P的列向量分别为ξ1,ξ2,…,ξn,则式(4.10)可写为
有(Aξ1 Aξ2 … Aξn)=(λ1ξ1 λ2ξ2 … λnξn),得
Aξ1=λ1ξ1,Aξ2=λ2ξ2,…,Aξn=λnξn. (4.11)
因为P为可逆矩阵,所以ξ1,ξ2,…,ξn都是非零向量,且ξ1,ξ2,…,ξn线性无关.由式(4.11)表明λ1,λ2,…,λn是矩阵A的特征值,ξ1,ξ2,…,ξn是A的分别对应于特征值λ1,λ2,…,λn的线性无关的特征向量,所以A有n个线性无关的特征向量.
再证充分性.设A有n个线性无关的特征向量ξ1,ξ2,…,ξn,假设它们对应的特征值分别为λ1,λ2,…,λn,有
Aξ1=λ1ξ1,Aξ2=λ2ξ2,…,Aξn=λnξn.
令矩阵P=(ξ1ξ2…ξn),则P为可逆矩阵,且
有
故A与对角矩阵Λ相似.
注意:从定理4.1的证明可以得到以下结论:
(1)可逆矩阵P就是以A的n个线性无关的特征向量ξ1,ξ2,…,ξn作为列向量构成的矩阵.
(2)对角矩阵Λ的主对角线上的元素λ1,λ2,…,λn是方阵A的特征值,且λ1,λ2,…,λn的排列顺序与它对应的特征向量ξ1,ξ2,…,ξn构成矩阵P的列向量时的排列顺序相一致.
例如,设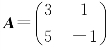 ,由本章例4.1知A有2个线性无关的特征向量,所以A一定可以相似对角化.事实上,因为A的特征值λ1=4,λ2=-2,对应的特征向量分别为
,由本章例4.1知A有2个线性无关的特征向量,所以A一定可以相似对角化.事实上,因为A的特征值λ1=4,λ2=-2,对应的特征向量分别为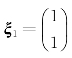 ,
,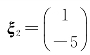 ,有
,有
如果取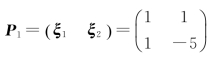 ,则
,则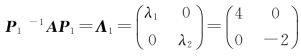 .
.
如果取![]() ,则
,则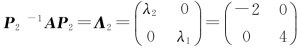 .
.
推论 若n阶方阵A有n个互异的特征值λ1,λ2,…,λn,则方阵A一定能与对角矩阵Λ相似,其中
注意:方阵A有n个互异的特征值只是A可以相似对角化的充分条件而不是必要条件.
例如,设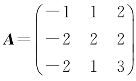 ,由本章例4.3知A有三个线性无关特征向量
,由本章例4.3知A有三个线性无关特征向量
这个例子说明当A有相同的特征值时,A也可以相似对角化.所以推论只是一个充分条件而非必要条件.
又例如,设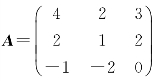 ,由本章例4.2知,A只能找到二个线性无关的特征向量,所以A不能相似对角化,此时A的对应于二重特征值λ=1的线性无关的特征向量个数仅为1.
,由本章例4.2知,A只能找到二个线性无关的特征向量,所以A不能相似对角化,此时A的对应于二重特征值λ=1的线性无关的特征向量个数仅为1.
于是我们给出下述定理:(https://www.daowen.com)
定理4.2 n阶方阵A能与n阶对角矩阵相似的充分必要条件是矩阵A的每个ni重特征值λi所对应的线性无关的特征向量个数恰好是ni个.
定理4.2 也可以等价地如下表述.
定理4.3 n阶方阵A能与n阶对角矩阵相似的充分必要条件是对于A的每个ni重特征值λi,有R(λiE-A)=n-ni.
[例4.7] 设矩阵 ,试求:
,试求:
(1)可逆矩阵P及对角矩阵Λ,使得P-1AP=Λ.(2)Am.
解 (1)A的特征多项式
所以A的特征值为λ1=λ2=0,λ3=-2.
当λ1=λ2=0时,解特征方程组(0E-A)X=0,
由
得基础解系为
当λ3=-2时,解特征方程组(-2E-A)X=0,
由
得基础解系为
于是3阶矩阵A有三个线性无关的特征向量,所以A可以相似对角化.令
则
(2)因为P-1AP=Λ,于是A=PΛP-1,有Am=PΛmP-1.又
所以
注意:把矩阵A先相似对角化再求Am,是计算矩阵的高次幂的基本方法之一.
[例4.8] 已知3阶方阵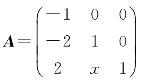 可以与对角矩阵相似,求x的值.
可以与对角矩阵相似,求x的值.
解 A的特征多项式
所以A的特征值为λ1=-1,λ2=λ3=1.
对应单根λ1=-1,可求得线性无关的特征向量恰有1个,故矩阵A可以相似对角化的充要条件是对应二重特征根λ2=λ3=1的线性无关的特征向量个数应为2个,则R(E-A)=1.由
知,要使R(E-A)=1,必须x=0.因此,当x=0时,A可相似对角化.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




