定义4.3 设A和B是n阶方阵,如果存在一个n阶可逆矩阵P,使得
P-1AP=B (4.9)
成立,则称矩阵A相似于矩阵B,或称B是A的相似矩阵.
可以验证:对于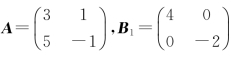 ,有
,有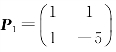 ,使得
,使得
所以A与B1相似,即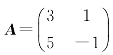 与
与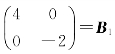 相似.
相似.
又若![]() ,有
,有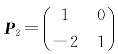 ,使得
,使得
所以A与B2相似,即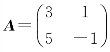 与
与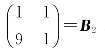 相似.
相似.
由定义可得,与一个方阵A相似的方阵并不唯一,相似是方阵之间的一种关系,设A,B,C均为n阶方阵,则相似关系还具有如下三种性质:
(1)反身性 A与A相似.
(2)对称性 若A与B相似,则B与A相似.
(3)传递性 若A与B相似,且B与C相似,则A与C相似.
证 (1)取P=E,则E-1AE=A,即A与A相似.
(2)由于A与B相似,故存在可逆矩阵P,使得P-1AP=B,则
(P-1)-1B(P-1)=A,
即B与A相似.
(3)由于A与B相似,且B与C相似,故存在可逆矩阵P1,P2,使得
P1-1AP1=B,P2-1BP2=C,
可得
C=P2-1BP2=P2-1P1-1AP1P2=(P1P2)-1A(P1P2),
即A与C相似.
彼此相似的矩阵还具有如下性质:
性质1 相似矩阵有相同的行列式.(www.daowen.com)
证 若A与B相似,则存在可逆矩阵P,使得P-1AP=B,两边取行列式,得
推论 相似矩阵或同时可逆,或同时不可逆,且当它们可逆时,它们的逆矩阵也相似.
证 设A与B相似,由本节性质1,知![]() ,所以A与B或同时可逆,或同时不可逆.
,所以A与B或同时可逆,或同时不可逆.
现设A与B均可逆,因为A与B相似,则存在可逆矩阵P,使得
P-1AP=B,
两边取逆,得
B-1=(P-1AP)-1=P-1A-1P,
即A-1与B-1相似.
性质2 相似矩阵有相同的特征多项式和特征值.
证 设A与B相似,则存在可逆矩阵P,使得P-1AP=B,故
即A与B有相同的特征多项式,从而A与B有相同的特征值.
性质3 相似矩阵有相同的秩.
证 设A与B相似,则存在可逆矩阵P,使得P-1AP=B,由2.6节定理2.7的推论2得R(A)=R(B).
注意:上述三条性质为矩阵相似的必要条件而非充分条件.例如矩阵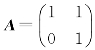 ,B=
,B=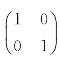 ,它们有相同的特征值λ1=λ2=1,但A与B不相似.事实上,若B与A相似,则存在可逆矩阵P,使得
,它们有相同的特征值λ1=λ2=1,但A与B不相似.事实上,若B与A相似,则存在可逆矩阵P,使得
A=P-1BP=P-1EP=E
与A≠E矛盾,所以A与B不相似.此例表明:单位矩阵只与自己相似.进一步讨论还可得:数量矩阵也只与自己相似.
由上面的讨论知道,相似矩阵具有很多共同的性质.对于n阶方阵A,自然希望找到一个既简单又便于计算的与A相似的矩阵.但由上面的讨论已经知道单位矩阵和数量矩阵都只能与自己相似,退而求其次,我们考虑比数量矩阵稍微复杂一些的“最简单”的矩阵,这就是对角矩阵.下面讨论一个n阶方阵A能否与一个对角矩阵相似的问题,即所谓的矩阵相似对角化问题,具体地说,就是讨论如下问题:
(1)是否所有的方阵都能与对角矩阵相似?若不能,则需满足怎样的条件,才能使一个方阵与一个同阶对角矩阵相似?
(2)如果一个方阵能与一个同阶对角矩阵相似,即存在可逆矩阵P,使得P-1AP为对角矩阵,那么怎样求得可逆矩阵P?
(3)如果一个方阵能与一个同阶对角矩阵相似,那么此对角矩阵的具体形式是什么?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






