性质1　n阶矩阵A与它的转置矩阵AT有相同的特征值.

证　由（λE-A）T=（λE）T-AT=λE-AT，得

则A和AT有相同的特征多项式，所以它们的特征值均相同.

性质2　设n阶矩阵A=（aij）的n个特征值为λ1，λ2，…，λn，则有

其中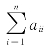为矩阵A的主对角线上元素之和，也称为矩阵A的迹，记为tr（A）.

证　记f（λ）=，一方面将行列式

按定义展开，其主对角线上元素的乘积项为

(λ-a11)(λ-a22)…(λ-ann).　(4.3)

而展开式中其余各项至多包含n-2个主对角线上元素，因而λ的次数最多为n-2，所以特征多项式f（λ）中含λn和λn-1的项只能出现在式（4.3）中，而f（λ）的常数项为f（0）=（-1）n，所以

另一方面，因为A的全部特征值为λ1，λ2，…，λn，故有

f(λ)=(λ-λ1)(λ-λ2)…(λ-λn)

=λn-(λ1+λ2+…+λn)λn-1+…+(-1)nλ1λ2…λn.　(4.5)

比较式（4.4）和式（4.5）右端λn-1的系数及常数项，可得

[例4.5]　设3阶矩阵，已知A有特征值λ1=1，λ2=2，试求x的值和A的另一特征值λ3.

解　根据本节性质2，有

而

故可得到

3+λ3=x+2,2λ3=x+2,

由此解得x=4，λ3=3.

推论　n阶矩阵A可逆的充分必要条件是A的n个特征值均不等于零.

性质3　若λ是n阶矩阵A的特征值，ξ是A的对应于特征值λ的特征向量，则

（1）kλ是矩阵kA的特征值，其中k是任意常数.

（2）λm是矩阵Am的特征值，其中m是正整数.

（3）g（λ）=a0+a1λ+a2λ2+…+amλm是矩阵

g(A)=a0E+a1A+a2A2+…+amAm

的特征值，其中m是正整数.

（4）当A可逆时，是A-1的特征值，为A的伴随矩阵A*的特征值.

证　由Aξ=λξ，得

（1）（kA）ξ=k（Aξ）=k（λξ）=（kλ）ξ，所以kλ是kA的特征值.

（2）A2ξ=A（A）ξ=A（λξ）=λ（Aξ）=λ2ξ，即A2ξ=λ2ξ；如此再继续上述步骤m-2次，得Amξ=λmξ，所以λm是Am的特征值.

(3)g(A)ξ=a0ξ+a1Aξ+a2A2ξ+…+amAmξ

=(a0+a1λ+a2λ2+…+amλm)ξ=g(λ)ξ,(www.daowen.com)

所以g（λ）是g（A）的特征值.

（4）当A可逆时，得λ≠0，则A-1（Aξ）=A-1（λξ）=λA-1ξ，即

所以是A-1的特征值.

由，得，所以是A伴随矩阵A*的特征值.

注意：由上述证明知道，若λ是n阶矩阵A的特征值，ξ是A的对应于特征值λ的特征向量，则矩阵kA，Am，g（A），A-1，A*的特征值分别是kλ，λm，g（λ），λ-1，，且ξ依然是矩阵kA，Am，g（A），A-1，A*的分别对应于特征值kλ，λm，g（λ），λ-1，的特征向量.

[例4.6]　设3阶矩阵A的特征值分别为-1、1、2，计算下列行列式的值.

解　因为-1、1、2是3阶矩阵A的特征值，所以=（-1）×1×2=-2.设λ是A的特征值，由本节中性质3（3）得λ3-2λ+1是A3-2A+E的特征值，是A*-A-1+A的特征值.则A3-2A+E的三个特征值分别为2、0、5，A*-A-1+A的三个特征值分别为2、-2、.所以

性质4　不同的特征值所对应的特征向量是线性无关的.

证　设λ1，λ2，…，λm是矩阵A的m个互不相同的特征值，ξ1，ξ2，…，ξm是分别对应于特征值λ1，λ2，…，λm的特征向量，即Aξi=λiξi，i=1，2，…，m.

下面用数学归纳法证明ξ1，ξ2，…，ξm线性无关.

当m=1时，因为特征向量ξ1是非零向量，而单个非零向量必定线性无关，所以结论成立.

假设m=k-1时结论成立，即分别对应于互异的特征值λ1，λ2，…，λk-1的k-1个特征向量ξ1，ξ2，…，ξk-1线性无关.

下面证明当m=k时结论也成立，即对应于k个互异的特征值λ1，λ2，…，λk的特征向量ξ1，ξ2，…，ξk线性无关.

设有一组数l1，l2，…，lk，使得

l1ξ1+l2ξ2+…+lkξk=0.　(4.6)

首先，式（4.6）两边同时左乘A，得

A(l1ξ1+l2ξ2+…+lkξk)=0.

因Aξi=λiξi，i=1，2，…，m，所以有

l1λ1ξ1+l2λ2ξ2+…+lkλkξk=0.　(4.7)

其次，在式（4.6）两边同时乘以λk，得

l1λkξ1+l2λkξ2+…+lkλkξk=0.　(4.8)

将式（4.8）减去式（4.7），得

l1(λk-λ1)ξ1+l2(λk-λ2)ξ2+…+lk-1(λk-λk-1)ξk-1=0.

由归纳法假设知ξ1，ξ2，…，ξk-1线性无关，于是

li(λk-λi)=0.

由于λ1，λ2，…，λk互不相同，所以λk-λi≠0，故必有li=0，其中i=1，2，…，k-1.于是式（4.6）化为lkξk=0，又ξk为非零向量，则lk=0，这就证明了ξ1，ξ2，…，ξk线性无关.根据归纳法，定理成立.

性质5　设λ1，λ2，…，λm是矩阵A的m个互不相同的特征值，ξi1，ξi2，…，ξiki是A的对应于特征值λi（i=1，2，…，m）的线性无关的特征向量，则由这些特征向量所组成的向量组

ξ11,ξ12,…,ξ1k1,ξ21,ξ22,…,ξ2k2,…,ξm1,ξm2,…,ξmkm

也是线性无关的.

证　略.