考虑如下问题：对于给定的n阶矩阵A，如何求出A的特征值和特征向量呢？它们之间的内在联系又是什么？下面我们从特征值与特征向量的定义出发来讨论这个问题.

如果λ为n阶矩阵A的特征值，ξ为A的对应于特征值λ的特征向量，则

Aξ=λξ,

即

(λE-A)ξ=0.

这就是说，特征向量ξ是n个方程n个未知量的齐次线性方程组

(λE-A)X=0　(4.2)

的非零解，且n阶方阵A的特征值λ使方程组（4.2）有非零解，即满足方程

的λ都是方阵A的特征值.于是，我们给出以下概念：

定义4.2　设n阶方阵

称n阶行列式

为矩阵A的特征多项式，它是关于λ的一个n次多项式，称方程为矩阵A的特征方程，称齐次线性方程组（λE-A）X=0为特征方程组.

由上面的讨论，可以得到求n阶方阵A的特征值与特征向量的步骤：

（1）求A的特征多项式.

（2）求出特征方程的所有根λ1，λ2，…，λn（其中可能有重根），它们就是矩阵A的全部特征值.

（3）对于A的每一个不同的特征值λj，求出相应的特征方程组（λjE-A）X=0的一个基础解系ξj1，ξj2，…，ξjt，它们是A的对应于特征值λj的一组线性无关的特征向量，而A的对应于特征值λj的全部特征向量为

kj1ξj1+kj2ξj2+…+kjtξjt,

其中kj1，kj2，…，kjt是不全为零的任意常数，j=1，2，…，m，其中m为矩阵A的相异的特征值个数.

[例4.1]　求矩阵的特征值与特征向量.

解　矩阵A的特征多项式为

令，所以λ1=4，λ2=-2是矩阵A的特征值.

当λ1=4时，解特征方程组（4E-A）X=0.由于

得同解方程组为

x1=x2

取x2=1，得到方程组的基础解系，即A的对应于λ1=4的线性无关的特征向量为

所以A的对应于λ1=4的全部特征向量为k1ξ11，其中k1为任意非零常数.

当λ2=-2时，解特征方程组（-2E-A）X=0.由于

得同解方程组为

取x2=5，得到方程组的基础解系，即A的对应于λ2=-2的线性无关的特征向量为(www.daowen.com)

所以A的对应于λ2=-2的全部特征向量为k2ξ21，其中k2为任意非零常数.

[例4.2]　求矩阵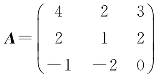的特征值与特征向量.

解　矩阵A的特征多项式为

令，所以λ1=λ2=1，λ3=3是矩阵A的特征值，其中λ1=λ2=1是矩阵A的二重特征值.

当λ1=λ2=1时，解特征方程组（E-A）X=0.由于

得同解方程组为

取x3=1，得到方程组的基础解系，即A的对应于λ1=λ2=1的线性无关的特征向量为

所以A的对应于λ1=λ2=1的全部特征向量为k1ξ11，其中k1为任意非零的常数.

当λ3=3时，解特征方程组（3E-A）X=0.由于

得同解方程组为

取x3=3，得到方程组的基础解系，即A的对应于λ3=3的线性无关的特征向量为

所以A的对应于λ3=3的全部特征向量为k2ξ21，其中k2为任意非零常数.

[例4.3]　求矩阵的特征值与特征向量.

解　矩阵A的特征多项式

令，所以λ1=λ2=1，λ3=2是矩阵A的特征值，其中λ1=λ2=1是矩阵A的二重特征值.

当λ1=λ2=1时，解特征方程组（E-A）X=0.由于

得同解方程组为

取，得A的对应于λ1=λ2=1的线性无关的特征向量为

所以A的对应于λ1=λ2=1的全部特征向量为k1ξ11+k2ξ12，其中k1，k2为不全为零的任意常数.

当λ3=2时，解特征方程组（2E-A）X=0.由于

得同解方程组为

取x3=1，得A的对应于λ3=2的线性无关的特征向量为

所以A的对应于λ3=2的全部特征向量为k3ξ21，其中k3为任意非零常数.

比较例4.2和例4.3可以看到，λ=1都是例4.2和例4.3中3阶矩阵A的二重特征根，但例4.2中A的对应于二重特征值λ=1的线性无关的特征向量只有1个，而在例4.3中A的对应于二重特征值λ=1的线性无关的特征向量有2个.由此看到r重特征值对应的线性无关的特征向量的个数小于或等于特征值的重数r，这一现象关系到本章第2节要讨论的方阵能否相似对角化.

[例4.4]　证明对角矩阵的主对角线上的元素是它的全部特征值.

证　设n阶对角矩阵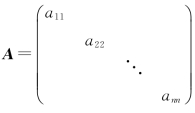，则A的特征多项式

令，故有λ1=a11，λ2=a22，…，λn=ann.所以对角矩阵的主对角线上的元素是它的全部特征值.

同理可知，n阶上（下）三角矩阵的主对角线上的元素也是对应三角矩阵的全部n个特征值.