对于线性方程组（3.1），我们利用新的概念——向量组的线性组合，可把方程组是否有解的问题转化为方程组的常数列向量能否由方程组的系数矩阵的列向量组线性表示的问题，借此可以很好解决方程组解的结构问题，此是后话.

与线性方程组（3.1）相仿，齐次线性方程组（3.3）可表示为

x1α1+x2α2+…+xnαn=0

此式称为齐次线性方程组（3.3）的向量式方程，其中α1，α2，…，αn是方程组的系数矩阵的列向量组.因

0·α1+0·α2+…+0·αn=0

必然成立，则齐次线性方程组（3.3）必有零解，所以我们更关注齐次线性方程组（3.3）除了零解以外的解——非零解是否存在，即是否存在一组不全为零的数k1，k2，…，kn，使得

k1α1+k2α2+…+knαn=0

成立.例如，齐次线性方程组

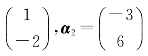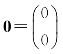除了有零解外，还有其他的解，如x1=3，x2=1，即方程组的系数矩阵的列向量组α1=与零向量间，显然有0·α1+0·α2=0成立，但也有3α1+α2=0成立，这说明向量α1，α2之间有某种“特殊”关系.而齐次线性方程组

只有零解，即方程组的系数组成的列向量组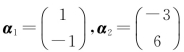与零向量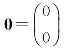间，只有0·α1+0·α2=0成立，这说明向量α1，α2之间没有某种“特殊”关系.

定义3.6　对于向量组α1，α2，…，αn，若存在不全为零的数λ1，λ2，…，λn，使得

λ1α1+λ2α2+…+λnαn=0　(3.5)

成立，则称向量组α1，α2，…，αn线性相关；否则，仅当λ1=λ2=…=λn=0时式（3.5）成立，则称向量组α1，α2，…，αn线性无关.

[例3.9]　设α1=（1，0，1）T，α2=（-1，2，2）T，α3=（1，2，4）T，试问向量组α1，α2及向量组α1，α2，α3的线性相关性各如何？

解　对向量组α1，α2，设λ1α1+λ2α2=0，即

可得

解得λ1=λ2=0，故向量组α1，α2线性无关.

对向量组α1，α2，α3，设λ1α1+λ2α2+λ3α3=0，即

可得

解得

取c=-1，得λ1=2，λ2=1，λ3=-1，则有

2α1+α2-α3=0

所以向量组α1，α2，α3线性相关.

从例3.9可进一步得到判别一个向量组的线性相关性的简便方法.

定理3.5　（1）m维向量组α1，α2，…，αn线性相关的充分必要条件是：以α1，α2，…，αn为列向量组成的矩阵A=（α1，α2，…，αn）的秩小于向量的个数n，即R（A）＜n.

（2）m维向量组α1，α2，…，αn线性无关的充分必要条件是：以α1，α2，…，αn为列向量组成的矩阵A=（α1，α2，…，αn）的秩等于向量的个数n，即R（A）=n.

推论　n个n维向量α1，α2，…，αn线性无关的充分必要条件是≠0；n个n维向量α1，α2，…，αn线性相关的充分必要条件是=0，其中A=（α1，α2，…，αn）.

解　记A=（α1，α2，α4），B=（α1，α2，α3，α4），则

因只对矩阵B作行初等变换，各列的次序没有改变，则从上述矩阵的第1、2、4列组成的矩阵可得R（A）=3，所以向量组A：α1，α2，α4线性无关；又因R（B）=3＜4，所以向量组B：α1，α2，α3，α4线性相关.

[例3.11]　证明下列命题：

（1）含有零向量的向量组必线性相关.

（2）只有一个零向量的向量组线性相关，只有一个非零向量的向量组线性无关.

（3）坐标单位向量组线性无关.

（4）如果向量组所含向量的个数大于向量组中向量的维数，则该向量组线性相关.(www.daowen.com)

证　（1）设含有零向量的向量组为α1，α2，…，αs，0，因为存在不全为零的数0，0，…，0，1，使得

0·α1+0·α2+…+0·αs+1·0=0

所以α1，α2，…，αs，0线性相关.

（2）因为对任意的k≠0，有k·0=0成立，所以一个零向量的向量组线性相关；而当一个向量α≠0时，当且仅当只有k=0时才有k·α=0成立，所以一个非零向量的向量组线性无关.

（3）因R（e1，e2，…，en）=R（En）=n，所以坐标单位向量组e1，e2，…，en线性无关.

（4）设向量组为n个m维向量所组成的向量组α1，α2，…，αn，且m＜n.记A=（α1，α2，…，αn），则R（A）≤min{m，n}=m＜n，所以该向量组线性相关.

[例3.12]　若向量组α1，α2，α3线性无关，则向量组α1+2α2，α2+3α3，α3+4α1也线性无关.

证　设有一组数k1，k2，k3，使得

k1(α1+2α2)+k2(α2+3α3)+k3(α3+4α1)=0　(3.6)

成立，整理可得

(k1+4k3)α1+(2k1+k2)α2+(3k2+k3)α3=0

因为向量组α1，α2，α3线性无关，则

易知该齐次线性方程组仅有零解，即只有k1=k2=k3=0时式（3.6）才成立，所以向量组线性无关.

定理3.6　如果向量组中有一部分向量组（称为部分组）线性相关，则整个向量组线性相关.

证　不妨设向量组α1，α2，…，αs，αs+1，…，αn中的部分组α1，α2，…，αs线性相关，其中s≤n，由向量组线性相关的定义，存在一组不全为零的数k1，k2，…，ks，使得

k1α1+k2α2+…+ksαs=0

成立.则存在一组不全为零的数k1，k2，…，ks，0，…，0，使得

k1α1+k2α2+…+ksαs+0·αs+1+…+0·αn=0

所以向量组α1，α2，…，αs，αs+1，…，αn线性相关.

推论　线性无关的向量组中的任一部分组必线性无关.

上述两结论给出了向量组中向量个数的增加与减少对向量组的线性相关性的影响.

定理3.7*　若m维向量组A：αj=（a1j，a2j，…，amj）T（j=1，2，…，n）线性无关，则此向量组在每个向量上添加k（k≥1）个分量后得到的m+k维的新的向量组（称为接长向量组）B：βj=（a1j，…，amj，am+1，j，…，am+k，j）T（j=1，2，…，n）也线性无关.

证　因为向量组A线性无关，则齐次线性方程组

x1α1+x2α2+…+xnαn=0

即

只有唯一零解.再考虑以向量组B：β1，β2，…，βn为系数列向量的齐次线性方程组

x1β1+x2β2+…+xnβn=0

即

在式（3.8）的m+k个方程中，前m个方程即为式（3.7）.因为方程组（3.7）只有唯一零解，所以方程组（3.8）也只有唯一零解，从而向量组B线性无关.

推论　若m维向量组α1，α2，…，αn线性相关，则将其每个向量去掉i（i＜m）个分量后得到的m-i维的新的向量组也线性相关.

上述两结论给出了向量组中向量维数的增加与减少对向量组的线性相关性的影响.