若干个同维的向量可组成一个向量组.

如e1=（1，0，…，0）T，e2=（0，1，…，0）T，…，en=（0，0，…，1）T是一个向量组，习惯上把e1，e2，…，en称为坐标单位向量组，简称单位向量组.

矩阵A=（aij）m×n的每一列（a1j，a2j，…，amj）T（j=1，2，…，n）即组成m维的一个向量组，称为矩阵A的列向量组.

矩阵A=（aij）m×n的每一行（ai1，ai2，…，ain）（i=1，2，…，m）即组成n维的一个向量组，称为矩阵A的行向量组.

线性方程组与向量组有以下关系：

线性方程组

的增广矩阵为

我们记第1至第4列为α1，α2，α3，α4，第5列为β，即

不难发现

x1α1+x2α2+x3α3+x4α4=β

即为原方程，只是表达形式改变了.

一般地，线性方程组（3.1）可表示为常数项组成的列向量与线性方程组的系数矩阵的列向量组有如下的线性关系式

x1α1+x2α2+…+xnαn=β

此式称为线性方程组（3.1）的向量形式，其中

均为m维向量.于是讨论线性方程组（3.1）是否有解，相当于讨论是否存在一组数x1=k1，x2=k2，…，xn=kn，使得表示式

k1α1+k2α2+…+knαn=β

成立，即常数项组成的列向量β是否可表示成方程组的系数矩阵的列向量组α1，α2，…，αn的线性表示式.如可以，则方程组有解；否则，方程组无解.基于此，定义如下：

定义3.4　设β，α1，α2，…，αs为一组n元向量，若存在一组数k1，k2，…，ks，使得

β=k1α1+k2α2+…+ksαs　(3.4)

成立，则称向量β是向量组α1，α2，…，αs的线性组合，或称向量β可由向量组α1，α2，…，αs线性表示（或线性表出）.

[例3.7]　（1）零向量可由任意一个同维向量组线性表示，因为

0=0·α1+0·α2+…+0·αs.

（2）任一n元向量α=（a1，a2，…，an）T可由n元单位向量组e1=（1，0，…，0）T，e2=（0，1，…，0）T，…，en=（0，0，…，1）T线性表示，即(www.daowen.com)

α=a1e1+a2e2+…+anen.

（3）向量组α1，α2，…，αs中的任一向量αj（j=1，2，…，s）都是此向量组的一个线性组合，因为αj=0·α1+0·α2+…+1·αj+…+0·αs.

(4)设α1=(1,0,2,-1)T,α2=(3,0,4,1)T,β=(-1,0,0,-3)T,因为β=2α1-α2,所以向量β可由向量组α1,α2线性表示.

如何判别向量β能否由向量组α1，α2，…，αs线性表示呢？从定义3.4易得下列结果.

定理3.4　向量β可由向量组α1，α2，…，αn线性表示的充分必要条件是：以向量组α1，α2，…，αn为系数矩阵列向量组，向量β为常数项列向量的线性方程组（3.1）有解，即

R(α1,α2,…,αn)=R(α1,α2,…,αn,β).

至于向量β可由向量组α1，α2，…，αn线性表示的表示式，只需解线性方程组

k1α1+k2α2+…+knαn=β

如果是唯一解，则说明表示式唯一；如果解不唯一，则说明表示式不唯一.

[例3.8]　设向量β1=（2，6，8，7）T，β2=（2，6，4，5）T，向量组A：

α1=（1，3，2，0）T，α2=（-2，-1，1，5）T，α3=（3，5，2，-4）T，α4=（-1，-3，-2，5）T问向量β1，β2能否由向量组A线性表示？

解　设β1=k1α1+k2α2+k3α3+k4α4，则该线性方程组的增广矩阵

因为R（A）=3，R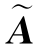（1）=4，所以向量β1不能由向量组A线性表示.

设β2=k1α1+k2α2+k3α3+k4α4，则该线性方程组的增广矩阵

因为R（A）=R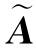（2）=3，所以向量β2能由向量组A线性表示.且从上式中可求得

其中c为任意常数；如取c=5，则可得β2由向量组A线性表示的一个表示式

β2=-4α1+4α2+5α3+α4.

定义3.5　如果向量组α1，α2，…，αs中的每一个向量都可以由向量组β1，β2，…，βt线性表示，则称向量组α1，α2，…，αs可由向量组β1，β2，…，βt线性表示；如果向量组α1，α2，…，αs与向量组β1，β2，…，βt可以互相线性表示，则称向量组α1，α2，…，αs与向量组β1，β2，…，βt等价.

向量组的等价关系是向量组与向量组之间的一种关系，易得这种等价关系满足：

（1）自反性　向量组α1，α2，…，αs与向量组α1，α2，…，αs等价.

（2）对称性　若向量组α1，α2，…，αs与向量组β1，β2，…，βt等价，则向量组β1，β2，…，βt也与向量组α1，α2，…，αs等价.

（3）传递性　若向量组α1，α2，…，αs与向量组β1，β2，…，βt等价，且向量组β1，β2，…，βt与向量组γ1，γ2，…，γp等价，则向量组α1，α2，…，αs也与向量组γ1，γ2，…，γp等价.