定理2.7　初等变换不改变矩阵的秩.

证　由于对矩阵作初等列变换就相当于对其转置矩阵作初等行变换，因而只需证明，作一次初等行变换不改变矩阵的秩即可.

由于k阶子式是行列式，利用行列式的性质，不难证明第一种与第二种初等行变换不改变矩阵的秩，下面仅就第三种初等行变换给出证明.设R（Am×n）=r，且按行分块有

先证明R（B）≤R（A）.只需证明矩阵B的所有r+1阶子式Mr+1=0.分以下三种情况：

（1）Mr+1不含B的第j行的元素，则Mr+1就是A的r+1阶子式，则Mr+1=0；

（2）Mr+1既含B的第j行的元素，同时也含B的第i行的元素，则由行列式的性质得Mr+1=0；

（3）Mr+1含B的第j行的元素，不含B的第i行的元素，则由行列式的性质必定有

Mr+1=M1+kM2,

其中M1是A的r+1阶子式，M2经过行重新排列也是A的r+1阶子式，且由行列式的性质得M2=0，故Mr+1=0.

综上，R（B）≤R（A）.

由于初等变换是可逆的，类似，可证R（A）≤R（B）.

综上讨论得R（A）=R（B），所以初等变换都不改变矩阵的秩.

推论1　若矩阵A与B等价，则R（A）=R（B）.

推论2　设A为m×n矩阵，P为m阶可逆矩阵，Q为n阶可逆矩阵，则

R(PA)=R(AQ)=R(PAQ)=R(A).

证　由于P可逆，则存在初等矩阵P1，P2，…，Ps，使得P=P1P2…Ps，而

PA=P1P2…PsA，即PA是由A经过s次初等变换得出的，故R（PA）=R（A）.(www.daowen.com)

同理可证，R（AQ）=R（PAQ）=R（A）.

由定理2.7可知：尽管初等变换改变了矩阵的外在形式，但是矩阵的一些最本质的内在性质却没有随之改变，矩阵的秩正是反映了矩阵固有的性质.

另外，利用定理2.7，可归纳出利用初等变换求矩阵的秩的方法，即把矩阵用初等行变换化为行阶梯形矩阵，则行阶梯形矩阵中非零行的行数就是该矩阵的秩.

[例2.28]　利用初等变换，求矩阵的秩.

[例2.29]　利用初等变换，求矩阵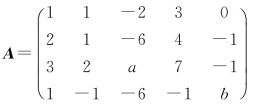的秩，其中a，b为未知常数.

（1）当a=-8且b=-2时，，所以R（A）=2；

（2）当a≠-8且b=-2时，，所以R（A）=3；

（3）当a=-8且b≠-2时，，所以R（A）=3；

（4）当a≠-8且b≠-2时，，所以R（A）=4.

[例2.30]　求矩阵的秩，其中λ为未知常数.

解　由于=（λ-1）2（λ+2），于是

（1）当λ≠1且λ≠-2时，≠0，故R（A）=3；

（2）当λ=1时，有，则R（A）=1；

（3）当λ=-2时，有，则R（A）=2.

[例2.31]　设4×3矩阵A的秩R（A）=2，，试求R（AB）.

解　，则R（B）=3，故B为可逆矩阵.由定理2.7的推论2，R（AB）=R（A）=2.