【摘要】:定义2.22设A为m×n矩阵,在A中任取k行k列(k≤min{m,n})交叉处的k2个元素,按原来的顺序构成一个k阶行列式,称为矩阵A的k阶子式.例如,在矩阵中,选择第1行、第2行和第2列、第4列,它们交叉位置上的元素构成行列式就是A的一个2阶子式.不难发现,m×n矩阵A共有个k阶子式.定义2.23设A为m×n矩阵,如果A中存在一个r阶子式不为零,而所有r+1阶子式(如果存在的话)全为零,那么
定义2.22 设A为m×n矩阵,在A中任取k行k列(k≤min{m,n})交叉处的k2个元素,按原来的顺序构成一个k阶行列式,称为矩阵A的k阶子式.
例如,在矩阵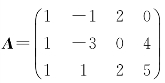 中,选择第1行、第2行和第2列、第4列,它们交叉位置上的元素构成行列式
中,选择第1行、第2行和第2列、第4列,它们交叉位置上的元素构成行列式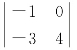 就是A的一个2阶子式.不难发现,m×n矩阵A共有
就是A的一个2阶子式.不难发现,m×n矩阵A共有![]() 个k阶子式.
个k阶子式.
定义2.23 设A为m×n矩阵,如果A中存在一个r阶子式不为零,而所有r+1阶子式(如果存在的话)全为零,那么称数r为矩阵A的秩,记为R(A),并规定零矩阵的秩为零.
根据矩阵的秩的定义,A的秩就是A中不为零的子式的最高阶数;若A为m×n矩阵,则
(1)0≤R(A)≤min{m,n}.
(2)R(AT)=R(A).
(3)R(λA)=R(A),其中λ≠0为常数.
特别地,对于n阶方阵A,若R(A)=n,称A为满秩矩阵;若R(A)<n,称A为降秩矩阵.显然,可逆矩阵是满秩矩阵,也是非奇异矩阵;不可逆矩阵是降秩矩阵,也是奇异矩阵.
[例2.26] 设矩阵 ,利用矩阵秩的定义,求A的秩.(https://www.daowen.com)
,利用矩阵秩的定义,求A的秩.(https://www.daowen.com)
解 A中存在二阶子式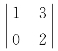 =2≠0,而更高阶的4个三阶子式
=2≠0,而更高阶的4个三阶子式
所以R(A)=2.
[例2.27] 设矩阵 ,利用矩阵秩的定义,求A的秩.
,利用矩阵秩的定义,求A的秩.
解 A中存在三阶子式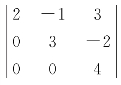 =24≠0,因第4行为零行,故四阶子式全为零,所以R(A)=3.
=24≠0,因第4行为零行,故四阶子式全为零,所以R(A)=3.
比较例2.26和例2.27,发现
(1)相对于一般矩阵而言,阶梯形矩阵的秩更容易求得;
(2)对于阶梯形矩阵,它的秩就等于它非零行的行数.
因此,考虑是否能借助初等变换将一般矩阵的求秩问题转化为阶梯形矩阵的求秩问题.这一转化的关键在于研究矩阵初等变换对矩阵的秩的影响.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章






