在本章3.3节中，给出的利用伴随矩阵求可逆矩阵的逆矩阵的方法，当遇到较高阶的矩阵求逆矩阵时，该方法计算量太大.下面介绍一种更为简便的方法，即用初等变换求逆矩阵的方法，称为初等变换法.

设n阶矩阵A可逆，则A-1也是可逆的，根据定理2.6的推论4，存在有限个n阶初等矩阵G1，G2，…，Gk，使得

A-1=G1G2…Gk,　(2.18)

用A右乘式（2.18）得

A-1A=(G1G2…Gk)A,

即

(G1G2…Gk)A=E.　(2.19)

由式（2.18），又有

(G1G2…Gk)E=A-1.　(2.20)

比较式（2.19）和式（2.20）可发现左乘初等矩阵G1G2…Gk可以将A转化成E，同时也可以将E转化为A-1.根据定理2.5，上述两式也表明：当用一系列初等行变换将可逆矩阵A化为单位矩阵E时，这同一组初等变换也能将单位矩阵E化为矩阵A-1.于是，可设计如下一种求逆矩阵的方法：

（1）构造一个n×2n的矩阵；

（2）利用初等行变换将中的子块A化为E，同时子块E就化为A-1；

（3）写出A的逆矩阵A-1.(www.daowen.com)

特别要注意，对实施的初等变换仅限于初等行变换.这个方法也可以简单地表示为

同理，也可以设计为仅利用初等列变换求逆矩阵，可以表示为

[例2.24]　利用初等变换法，求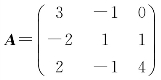矩阵的逆矩阵.

下面介绍利用初等变换法求解矩阵方程.

对于矩阵方程AX=B，若A可逆，则存在有限个n阶初等矩阵G1，G2，…，Gk，使得A-1=G1G2…Gk，故

E=A-1A=(G1G2…Gk)A,　(2.21)

又

X=A-1B=(G1G2…Gk)B.　(2.22)

比较式（2.21）、式（2.22），可知当用有限个初等行变换将A化为E时，这组初等行变换同时也能将B化为X，即

类似地，对于矩阵方程XA=B，其中A可逆，则X=BA-1，仅用列初等变换的求法可以表示为

[例2.25]　利用初等变换法，求解矩阵方程AX=B，其中

由此知A可逆，且