初等变换将一个矩阵变成了另一个矩阵，前后两个矩阵不是相等的关系，为了建立它们之间的变化关系式，就要研究初等变换与初等矩阵之间的关系.

例如，设矩阵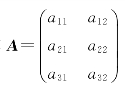，任意常数k≠0，则有

以及

比较式（2.14）和式（2.15）发现，矩阵B是A作一次第二类初等行变换的结果，同样也是在A的左边乘以一个第二类初等矩阵的结果.另有，

以及

比较式（2.16）和式（2.17）发现，矩阵C是A作一次第二类初等列变换的结果，同样也是在A的右边乘以一个第二类初等矩阵的结果.

一般地，有以下结论.

定理2.5　设A是一个m×n矩阵，

（1）对A作一次初等行变换，相当于在A的左边乘以一个同类的m阶初等矩阵；

（2）对A作一次初等列变换，相当于在A的右边乘以一个同类的n阶初等矩阵.

证　我们只看列变换的情形，行变换的情形可同样证明.令B=（bij）是任意一个n×n矩阵，将A按列分块成A=（A1，A2，…，An），由分块矩阵的乘法，得

特别地，令B=E（i，j），则

这相当于把A的第i列与第j列互换.类似地，可以证明另两个变换情况.

结合定理2.4和定理2.5，得到下面的结论.

定理2.6　设A是一个m×n矩阵，则存在m阶初等矩阵P1，P2，…，Ps和n阶初等矩阵Q1，Q2，…，Qt，使得

例2.23中矩阵A化为标准形的初等变换过程可利用下列关系式表示

推论1　设A为m×n矩阵，则存在m阶可逆矩阵P和n阶可逆矩阵Q，使得(www.daowen.com)

证　在定理2.6中，令P=PsPs-1…P1，Q=Q1Q2…Qt，显然P，Q都是可逆矩阵.

推论2　设A和B都是m×n矩阵，则A等价于B的充分必要条件是：存在m阶可逆矩阵P和n阶可逆矩阵Q，使得

PAQ=B.

该推论的证明请读者自行完成.

推论3　n阶矩阵A可逆，当且仅当A的标准形为单位矩阵En.

证　必要性：由推论1知，对n阶可逆矩阵A，存在n阶可逆矩阵P和Q，使得

将上式两边取行列式，有

若r＜n，有

这与产生矛盾，故r=n.

充分性：若n阶矩阵A的标准形为En，则由定理2.6知，存在有限多个n阶初等矩阵P1，P2，…，Ps和Q1，Q2，…，Qt，使得

Ps…P2P1AQ1Q2…Qt=En,

则有

显然，矩阵A是可逆矩阵.

推论4　n阶可逆矩阵A可以表示成有限个初等矩阵的乘积.

证　由推论3及其证明过程易证得.