由于对角矩阵形式简单，运算方便，因而也常将一些特殊的方阵分块成对角矩阵，再进行矩阵的运算.

定义2.15　设A为n阶矩阵，若将A分块后只在对角线上有非零子块，其余子块都为零矩阵，且对角线上的子块都是方阵，即

其中Ai（i=1，2，…，s）分别为ni阶方阵，则称A为分块对角矩阵，也记为A=diag（A1，A2，…，As）.

例如，矩阵

其中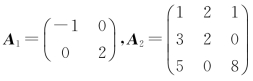，这样的分块方法就形成了分块对角矩阵.

分块对角矩阵具有类似于对角矩阵的运算性质.

设A，B为分法相同的同型分块对角矩阵，即

A=diag(A1,A2,…,At),B=diag(B1,B2,…,Bt)

则有如下性质

性质1　A±B=diag（A1±B1，A2±B2，…，At±Bt）.

性质2　kA=diag（kA1，kA2，…，kAt），其中k为实数.

性质3　AB=diag（A1B1，A2B2，…，AtBt）.

性质4　，其中k为正整数.

性质5　若Ai（i=1，2，…，t）均可逆，则.

性质6　.

性质7　.(www.daowen.com)

特别地，若

A=diag(a1,a2,…,at),B=diag(b1,b2,…,bt),

其中ai，bi（i=1，2，…，t）为实数，上述性质也成立，即

性质1′　A±B=diag（a1±b1，a2±b2，…，at±bt）.

性质2′　kA=diag（ka1，ka2，…，kat），其中k为实数.

性质3′　AB=diag（a1b1，a2b2，…，atbt）.

性质4′　，其中k为正整数.

性质5′　若ai≠0（i=1，2，…，t），则.

性质6′　AT=A.

性质7′　=a1·a2·…·at.

[例2.22]　设矩阵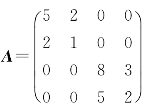，求和A-1.

解　将矩阵A分成，，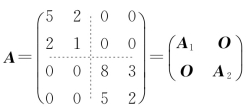

则

又

所以