矩阵的运算在以分块矩阵形式运算时会与原来的运算有一些变化.

（1）分块矩阵的加法

设分块矩阵A=（Akl）p×q，B=（Bkl）p×q，其中A与B的对应子块Akl和Bkl都是同型矩阵，则

（2）分块矩阵的数乘

设分块矩阵A=（Aij）p×q，k是一个实数，则

（3）分块矩阵的乘积

设A=（aij）m×l，B=（bij）l×n，按A的列的分法与B的行的分法相同的分块原则（A的行的分法与B的列的分法不限），把A与B分成

则AB=C=（Cij）r×s，其中

Cij=Ai1B1j+Ai2B2j+…+AitBtj　i=1,2,…,r;j=1,2,…,s.

特别要强调是，在进行两个分块矩阵的乘法运算时，左矩阵A的列的分法必须与右矩阵B的行的分法完全一致，即子块Ai1，Ai2，…，Ait各自的列数分别等于子块B1j，B2j，…，Btj各自的行数，其中i=1，2，…，r；j=1，2，…，s.

（4）分块矩阵的转置

设分块矩阵为

则A的转置矩阵为

注意　分块矩阵的转置，不但要把以子块为元素的行、列互换，且每个子块也要转置.(www.daowen.com)

合理地分块可以使矩阵内元素分布的特点更为清晰，运算更为简洁.

[例2.20]　设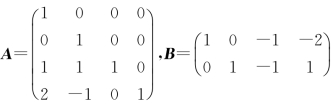.利用矩阵的分块，求BT和ABT.

解　把矩阵B分成

则

把矩阵A与BT分别进行如下的分块

则

[例2.21]　设方阵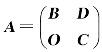，其中B和C都为可逆矩阵，证明：矩阵A可逆，并求A-1.

证　因为，所以A可逆.设A有逆矩阵，为H，将H按A的分块方法进行分块，并记

则有

得

由于B和C都为可逆矩阵，可解得

从本例可以看到，利用将矩阵分块进行求逆的方法，可以将高阶矩阵的求逆问题转化成低阶矩阵的求逆问题，从而大大减少计算量.