方阵的逆矩阵满足下述性质：

性质1　设A可逆，则A-1可逆，且（A-1）-1=A.

性质2　设A可逆，λ是非零实数，则λA可逆，且.

性质3　设A，B为n阶可逆矩阵，则AB可逆，且（AB）-1=B-1A-1.

此性质可推广到有限多个矩阵的情形，即若A1，A2，…，Ak都是n阶可逆矩阵，则A1A2…Ak也可逆，且

(A1A2…Ak)-1=Ak-1…A2-1A1-1.

性质4　设A可逆，则AT可逆，且（AT）-1=（A-1）T.

性质5　设A可逆，则.

性质6　（1）设A可逆时，则A*可逆，且.

（2）设A为n阶矩阵，则.

下面我们证明性质3和性质6，其余的利用可逆矩阵的定义易证得.

证　先证明性质3.由（AB）（B-1A-1）=A（BB-1）A-1=AEA-1=AA-1=E，得AB可逆，且(www.daowen.com)

(AB)-1=B-1A-1.

再证明性质6中的（1）.根据定理2.1有

当A可逆时，≠0，故

因此，A*可逆且.

最后证明性质6中的（2）.将式（2.11）两边取行列式，得

下面分A可逆与A不可逆两种情况讨论.

当A可逆时，≠0，故由式（2.12）得.

当A不可逆时，=0.又分两种情况：若A=O，则A*=O，有=0，则；若A≠O，假设≠0，则A*可逆.由AA*=E，得AA*=O.等式两边右乘以（A*）-1，得A=O，与A≠O矛盾，所以=0，这时也有.

[例2.19]　设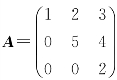，求（A*）-1.

解　=10，则