下面研究逆矩阵存在的条件.

定理2.3　n阶方阵A可逆的充分必要条件是≠0，且当A可逆时，有

证　必要性：由A可逆，有AA-1=E，故

所以≠0.

故A可逆，且.

习惯上，如果≠0，则称A为非奇异矩阵；如果=0，则称A为奇异矩阵.显然，可逆矩阵是非奇异矩阵.

定理2.3不但给出了矩阵可逆的充要条件，而且提供了一种用伴随矩阵求逆矩阵的方法.利用公式（2.10）求逆矩阵的方法称为伴随矩阵法.

[例2.12]　设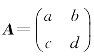，且ad-bc≠0，求A-1.

解　=ad-bc≠0，则A-1存在.又

由式（2.10），得

[例2.13]　解矩阵方程：.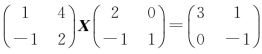

解　令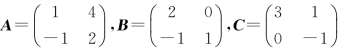，可求得，故A，B都是可逆的.因此，在矩阵方程AXB=C两端同时左乘A-1、右乘B-1，得

X=A-1CB-1,

即

由例2.12得.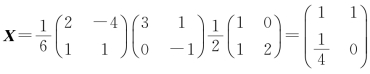

[例2.14]　设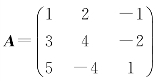，用伴随矩阵法求A-1.

解　因=2≠0，故A可逆.计算得

A11=-4,　A21=2,　A31=0,

A12=-13,　A22=6,　A32=-1,

A13=-32;　A23=14;　A33=-2,

则(www.daowen.com)

所以

[例2.15]　设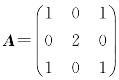，方阵X满足矩阵方程X=AX-A2+E，求X.

解　因为X=AX-A2+E，进而（E-A）X=E-A2，即

(E-A)X=(E-A)(E+A).

由于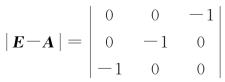=1≠0，故E-A是可逆的.用（E-A）-1同时左乘等式两端，得X=E+A，最后求得

推论　若n阶矩阵A和B满足AB=E（或BA=E），则A可逆，且B为A的逆矩阵.

证　若AB=E，则，从而≠0.根据定理2.3，A可逆且

A-1=A-1E=A-1(AB)=(A-1A)B=EB=B.

同理可证BA=E的情况.

利用这个推论，证明B为A的逆矩阵变得更为方便，只需验证等式AB=E、BA=E中的一个等式成立即可，而不必按定义验证两个等式.

[例2.16]　设方阵A满足等式A2-A-2E=O，证明A+2E可逆，并求（A+2E）-1.

证　由A2-A-2E=O，得

(A+2E)(A-3E)=-4E,

故有

所以A+2E可逆且.

[例2.17]　设n阶方阵A和B满足A+B=AB，证明A-E可逆，并求（A-E）-1.

证　由A+B=AB，得AB-A-B=O，进而AB-A-B+E=E，即

(A-E)(B-E)=E,

所以A-E可逆且（A-E）-1=B-E.