定义2.13　设A为n阶方阵，如果存在n阶方阵B，使得

AB=BA=E　(2.7)

则称矩阵A是可逆矩阵（或称A是可逆的），并称B是A的逆矩阵，记为A-1，即A-1=B.

例如：记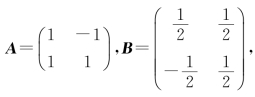容易验证它们满足AB=BA=E，则可说A是可逆的且B是A的逆矩阵，同样也可以说B是可逆的且A是B的逆矩阵.

下面的定理解决了可逆矩阵的逆矩阵的个数问题.

定理2.2　可逆矩阵的逆矩阵是唯一的.

证　设矩阵B，C分别是可逆矩阵A的逆矩阵，则有AC=CA=E及AB=BA=E.

因此，有

B=BE=B(AC)=(BA)C=EC=C,

故A的逆矩阵是唯一的.(www.daowen.com)

在研究逆矩阵中要注意的是：

（1）可逆矩阵和它的逆矩阵是同阶的方阵；

（2）可逆矩阵和它的逆矩阵地位平等，故它们是一种互逆关系；

（3）可逆矩阵A的逆矩阵记号是A-1，而绝不能用.

下面的例子，有助于从线性变换的角度更好地理解逆矩阵的概念.

[例2.11]　设线性变换

及

其中λi≠0（i=1，2，…，n）.显然，线性变换式（2.9）是线性变换式（2.8）的逆变换.从矩阵的角度可以看到，线性变换式（2.8）和式（2.9）对应的矩阵分别为

并且满足AB=BA=E.