定义2.7　把m×n矩阵

的行列依次互换得到的一个n×m矩阵，称为矩阵A的转置矩阵，记为AT或A′，即

例如，

矩阵的转置满足以下规律：（假设以下运算均可行）

(1)(AT)T=A.

（2）（kA）T=kAT，其中k为实数.

(3)(A±B)T=AT±BT.

(4)(AB)T=BTAT.

将（3）和（4）推广到有限多个矩阵的情形，有

(A1±A2±…±Ak)T=A1T±A2T±…±AkT.

(A1A2…Ak)T=AkT…A2TA1T.

证　前三式易证，下面仅证（4）.

设A=（aij）m×s，B=（bij）s×n，显然（AB）T和BTAT都是n×m矩阵.

记C=AB=（cij）m×n，D=BTAT=（dij）n×m，于是C在第j行第i列的元素为

故CT在第i行第j列的元素为

另一方面，BT的第i行为（b1i，b2i，…，bsi），AT的第j列为（aj1，aj2，…，ajs）T，则

于是

(AB)T=BTAT.

定义2.8　设A为n阶矩阵，如果

（1）AT=A，则称A为对称矩阵；

（2）AT=-A，则称A为反对称矩阵.(www.daowen.com)

例如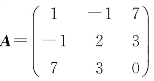：是对称矩阵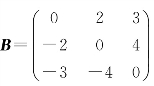，是反对称矩阵.

由定义易得，对称矩阵和反对称矩阵有下面的性质：

（1）A=（aij）n×n为对称矩阵的充要条件是aij=aji（i，j=1，2，…，n）.

（2）A=（aij）n×n为反对称矩阵的充要条件是aij=-aji（i，j=1，2，…，n）.

注意　对称矩阵和反对称矩阵都是方阵.反对称矩阵主对角线上元素全为零.

[例2.6]　设A为n阶矩阵，证明A+AT为对称矩阵，A-AT为反对称矩阵.

证　因为

(A+AT)T=AT+(AT)T=AT+A,

根据定义2.8（1）知A+AT为对称矩阵.又

(A-AT)T=AT-(AT)T=AT-A=-(A-AT),

根据定义2.8（2）知A-AT为反对称矩阵.

由于任意的n阶矩阵A可以表示为

故结合上例可知，任意n阶矩阵都可表示为一个对称矩阵与一个反对称矩阵的和.

[例2.7]　设列矩阵X=（x1x2…xn）T满足XTX=1，H=E-2XXT，证明：H为对称矩阵且HHT=E.

证　HT=（E-2XXT）T=ET-（2XXT）T=E-2（XT）TXT=E-2XXT=H，所以H为对称矩阵.

HHT=H2=(E-2XXT)2=E-4XXT+4(XXT)2

=E-4XXT+4X(XTX)XT=E-4XXT+4XXT=E.

上例中要特别注意的是是数，而

是一个n阶的方阵.