根据矩阵中元素或形状的特点，分别命名以下几类常用的特殊矩阵：

（1）复矩阵　元素是复数的矩阵称为复矩阵.

（2）实矩阵　元素为实数的矩阵称为实矩阵.本书中的矩阵如无特殊说明，都指实矩阵.

（3）零矩阵　元素都是零的矩阵称为零矩阵，记作O.要注意的是不同型的零矩阵是不相等的.

（4）行矩阵（或行向量）　仅有一行的矩阵称为行矩阵（也称为行向量），行矩阵

A=(a11a12…a1n)

也可用希腊字母记为α=（a11a12…a1n）.

（5）列矩阵（或列向量）　仅有一列的矩阵称为列矩阵（也称为列向量），列矩阵

也可用希腊字母记为.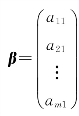

（6）方阵　行数与列数相等的矩阵称为方阵，如

称为n阶方阵或n阶矩阵，简记为A=（aij）n.从左上角到右下角的连线称为方阵的主对角线.(www.daowen.com)

（7）三角矩阵　主对角线以下（或上）的元素全为零的方阵称为上（或下）三角矩阵.

通常对于矩阵中零元素集中的部分可以将零元素省略不写或集中用O表示.如

为n阶上三角矩阵；而矩阵

为n阶下三角矩阵.

（8）对角矩阵　除主对角线上元素外，其他元素全为零的方阵称为对角矩阵.如

为n阶对角矩阵，记为Λ或diag（λ1，λ2，…，λn）.

（9）数量矩阵　主对角线上的元素相等，其他元素全为零的对角矩阵称为数量矩阵.如

为n阶数量矩阵，记为kEn或kE.

（10）单位矩阵　主对角线上的元素全为1，其他元素全为零的数量矩阵称为n阶单位矩阵，记为En，简记为E，即

注意　不同阶的单位矩阵是不相等的.