直接用行列式的定义计算行列式，在一般情况下比较烦琐.本节先研究行列式的一些性质，这些性质有助于我们了解行列式的特点，从而更方便地计算行列式.

定义1.8　设n阶行列式，则将D的行依次变为相应的列，所得到的n阶行列式称为D的转置行列式，记作DT，即

性质1　行列式与它的转置行列式的值相等，即D=DT.

证　设，且记

则有

bij=aji(i,j=1,2,…,n).　(1.19)

将DT按式（1.17）展开，并将式（1.19）代入，与式（1.18）比较，得

性质1说明，行列式中行与列具有同等的地位，也就是说行列式的性质凡是对行成立的对列也成立，反之亦然.因此，在证明行列式性质时，只需证明对行成立即可.

性质2　交换行列式的任意两行（列），行列式的值变号.

证　设

交换D1的第s行和第t行，得到行列式

将D1和D2分别按式（1.17）展开，得到

对比展开式（1.20）和（1.21），由于排列经过一次对换奇偶性改变，故可得D1=-D2.

推论　如果行列式中有两行（列）对应元素相同，则该行列式的值为零.

证　显然，将行列式D中具有相同对应元素的两行互换，其结果仍为D.但是根据性质2，D中具有相同对应元素的两行互换，结果为-D.则有D=-D，故D=0.

性质3　行列式某一行（列）的所有元素都乘以数k，等于用数k乘以此行列式，即

证　由行列式定义，

推论1　行列式某一行（列）所有元素的公因子可以提到行列式记号外.

推论2　若行列式某一行（列）的元素都为零，则此行列式的值为零.

推论3　若行列式中某两行（列）对应元素成比例，则此行列式的值为零.

性质4　若行列式的某一行（列）的元素都是两数之和，则此行列式可以写成两个行列式的和，这两个行列式分别以这两个数为所在行（列）对应位置的元素，其他位置的元素与原行列式相同.即若设

则D=D1+D2.

证　只证性质对行成立.由行列式定义，

性质5　行列式的某一行（列）各元素乘以同一数后加到另一行（列）对应元素上去，行列式的值不变.即若设

将D的第i行元素乘以数k加到第s行元素对应位置的元素上，得到

则D=D1.

证　由性质4及性质3的推论3，得

在行列式的计算中，通常约定用字母ri表示行列式的第i行，字母cj表示行列式的第j列，并且引入以下记号：

（1）用ri↔rj表示第i行与第j行互换，用ci↔cj表示第i列与第j列互换；(www.daowen.com)

（2）用kri表示用数k乘以行列式的第i行，用kci表示用数k乘以行列式的第i列；

（3）用rj+kri表示用数k乘以行列式的第i行的各元素加到第j行上去，用cj+kci表示用数k乘以行列式的第i列的各元素加到第j列上去.

[例1.8]　设3阶行列式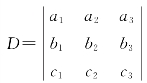=M≠0，求下列行列式的值.

解　（1）由性质1，D1=D=M.

（2）由性质2，

（3）由性质2，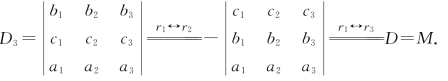

（4）由性质2的推论，D4=0.

（5）由性质3，

（6）由性质3，

（7）方法一

方法二

在例1.8的（6）中要特别注意，利用性质3提取公因子时，是按一行（列）提取的.而在（8）中要注意的是若利用性质4将D8完全分拆开，应得到8个行列式之和.

因为三角行列式容易计算，所以在行列式的计算中，常利用行列式的性质将它化为三角行列式进行计算，这种方法称为化三角法.

[例1.9]　利用化三角法，计算行列式.

[例1.10]　利用化三角法，计算n+1阶行列式.

解　将D的第2，3，…，n+1列都加到第1列，再提取公因子，得

再将第1列的-aj倍分别加到第j+1列（j=1，2，…，n），得

[例1.11]　计算爪形行列式

其中未写出的元素为零.

解　将D的第j列的倍都加到第1列（j=2，3，…，n），得

[例1.12]　设

利用化三角法，证明：D=D1D2.

证*　对D1作适当的行运算ri+krj，可把D1化为下三角行列式

对D2作适当的列运算ci+k′cj，可把D2化为下三角行列式

因此，先对D的前k行作行运算ri+krj，然后对D的后n列作列运算ci+k′cj，把D化为下三角行列式

故，，即

同理，可以证明

以上两个结论可以作为公式使用.