设三元线性方程组的一般形式为

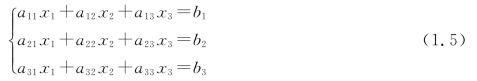
当a11a22a33+a12a23a31+a13a21a32-a11a23a32-a12a21a33-a13a22a31≠0时，仍然利用消元法，可以得到方程组式（1.5）解的一般公式为

上述表达式记起来非常困难，为此引入3阶行列式.

定义1.2　称记号

为3阶行列式，用它表示代数和

a11a22a33+a12a23a31+a13a21a32-a11a23a32-a12a21a33-a13a22a31,

即

式（1.7）称为3阶行列式的展开式.

在展开式（1.7）中，可以看到3阶行列式的值是3！项乘积的代数和，其中3项是正号，3项是负号，且每项都是不同行、不同列的3个元素的乘积.

式（1.7）可以用图1.2所示的画线方法帮助记忆，即3阶行列式的值等于其中三条实线联结的3个元素乘积之和与三条虚线连接的3个元素乘积之和的差，这个法则也称为3阶行列式的对角线法则.

类似二元线性方程组，记

图1.2(www.daowen.com)

当D≠0时，方程组（1.5）解的公式（1.6）就可以方便地表示为

其中Dj（j=1，2，3）是用线性方程组（1.5）的常数项b1，b2，b3替代D中第j列相应的元素所得到的3阶行列式.

[例1.2]　计算3阶行列式.

解　由3阶行列式的对角线法则，得

D=1×2×2+(-2)×1×3+3×2×0-3×2×3-(-2)×2×2-1×0×1=-12.

[例1.3]　利用行列式求解三元线性方程组

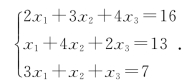
解　由3阶行列式的对角线法则，得=-25≠0，

由式（1.8）得方程组的解为

从以上叙述可以看出，引入2、3阶行列式的概念后，为表示和记忆二、三元线性方程组的解的公式带来了极大的便利.但是在实际问题中遇到的线性方程组，未知量往往不止三个，为把上述结果推广到n个方程、n个未知量的线性方程组

需要引入n阶行列式的定义.