【摘要】:设二元线性方程组用消元法解此方程组,得当a11a22-a12a21≠0时,可求得式(1.1)方程组的唯一解为式(1.2)给出了二元线性方程组式(1.1)解的一般公式,但它难以记忆,因而有必要引入一个符号来更方便地表示,这就有了行列式.定义1.1称记号为2阶行列式,用它表示代数和a11a22-a12a21,即式(1.3)称为2阶行列式的展开式,其中aij称为2阶行列式的元素,第一个下标i称为行标,
设二元线性方程组

用消元法解此方程组,得
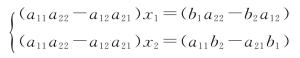
当a11a22-a12a21≠0时,可求得式(1.1)方程组的唯一解为

式(1.2)给出了二元线性方程组式(1.1)解的一般公式,但它难以记忆,因而有必要引入一个符号来更方便地表示,这就有了行列式.
定义1.1 称记号
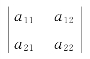
为2阶行列式,用它表示代数和a11a22-a12a21,即
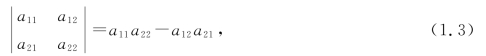
式(1.3)称为2阶行列式的展开式,其中aij称为2阶行列式的元素,第一个下标i称为行标,第二个下标j称为列标,它们表示aij位于行列式中的第i行第j列(横排叫行,纵排叫列).
式(1.3)可以用图1.1所示的画线方法帮助记忆.将左上角与右下角的连线(实线)称为行列式的主对角线,将右上角与左下角的连线(虚线)称为副对角线(或次对角线).那么式(1.3)就可以被方便地表述为:2阶行列式等于主对角线上元素的乘积与副对角线上元素的乘积之差,这个方法称为2阶行列式的对角线法则.(www.daowen.com)
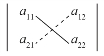
图1.1
引入了2阶行列式后,式(1.2)中的分子和分母可以分别记为
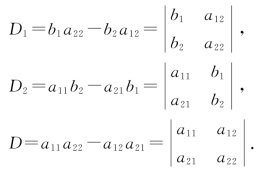
那么当D≠0时,方程组式(1.1)的解式(1.2)就可以很方便、简洁地表示为
![]()
特别,还可以注意到其中Dj(j=1,2)分别是用线性方程组(1.1)的常数项b1,b2取代了D中第j列元素得到的2阶行列式.
[例1.1] 利用行列式求解2元线性方程组
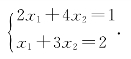
解 由于
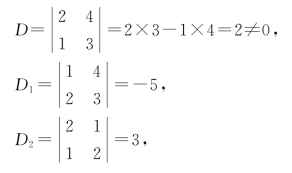
因此方程组的解为
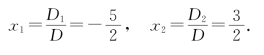
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关工程数学的文章







