1.液体的流量

液体在管道中流动时，垂直于液体流动方向的截面称为通流截面。单位时间内流过某通流截面的液体体积称为流量，用q_v表示。即

q_v=V/t

单位为m³/s或L/min，换算1m³/s=6×10⁴L/min。

假设通流截面上各点的流速均匀分布，流速是指液流质点在单位时间内流过的距离，用v表示，即v=s/t，单位为m/s或m/min。若把上式分子分母各乘以通流截面积A则得

v=sA/（tA）=q_v/A

即q_v=vA，液体以流速v流过通流截面A的流量等于流速v和通流截面积A的乘积。在液压缸中液体的流速可以认为是均匀分布的（液体流动速度与活塞运动速度相同）。当液压缸的有效工作面积A一定时，活塞运动速度v便取决于输入液压缸的流量q_v。

2.液流的连续性(www.daowen.com)

液体的可压缩性很小，一般可忽略不计。因此，液体在管内作稳定流动（流动液体中任一点的压力、速度和密度都不随时间而变化），根据质量守恒定律，在单位时间内管中每一个通流截面的液体质量是相等的，这就是液流的连续性原理。如图4-6所示，液体在不等截面的管中流动，设通流截面1和2的直径各为d₁和d₂，面积各为A₁和A₂，平均流速分别为v₁和v₂，两个通流截面处液体的密度都为ρ，根据液流的连续性原理，流经截面1和2的液体质量应相等。即

ρ^v₁A₁=ρv₂A₂=ρvA=常量

上式称为液流的连续性方程式，将上式化简得

v₁A₁=v₂A₂=vA=常量

上式表明流体在管中流动时流过各个通流截面的流量是相等的，即q_v1=q_v2=常量。因而流速和通流面积成反比，管粗流速低，管细流速快。

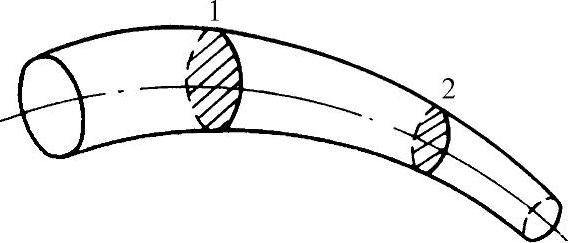
图4-6 液流的连续性简图