本节将结合HMM情感模型与Baum-Welch算法，应用于双足机器人步态的情感模型建立。

1.情感模型的传递

机器人整体传递系统由两大类组成，即输入端和输出端，具体如图6-4所示。输入端是通过情感模型空间对外界刺激进行反应，输出端是机器人通过情感认知系统进行步态姿势输出。整体构成了机器人情感接收和反应的过程，包括情感因子的提取和分析。除此之外还有外界情感刺激，情感模型与步态姿势的对应等。

2.基于HMM的情感建模

我们首先要确定情感的每个层次上的种类数量，即HMM中对应的状态数n和心情种类对应的个数m。在每种心情中，各种状态以一定概率出现。HMM由两部分组成，一个为马尔可夫链，由π和A描述（π为初始状态概率矢量，A为状态概率转移矩阵），它们决定了马尔可夫链的形状。其中，马尔可夫链为状态遍历类型，严格来说，遍历模型的性质是任何一个状态可由任一个其他状态在有限步内到达。此类模型性质为每个a_ij系数都是正的，即对任意i，j，有a_ij>0。HMM另一组成部分由B描述，B为观察概率矩阵，产生的输出为观察值序列。HMM的组成如图6-5所示。

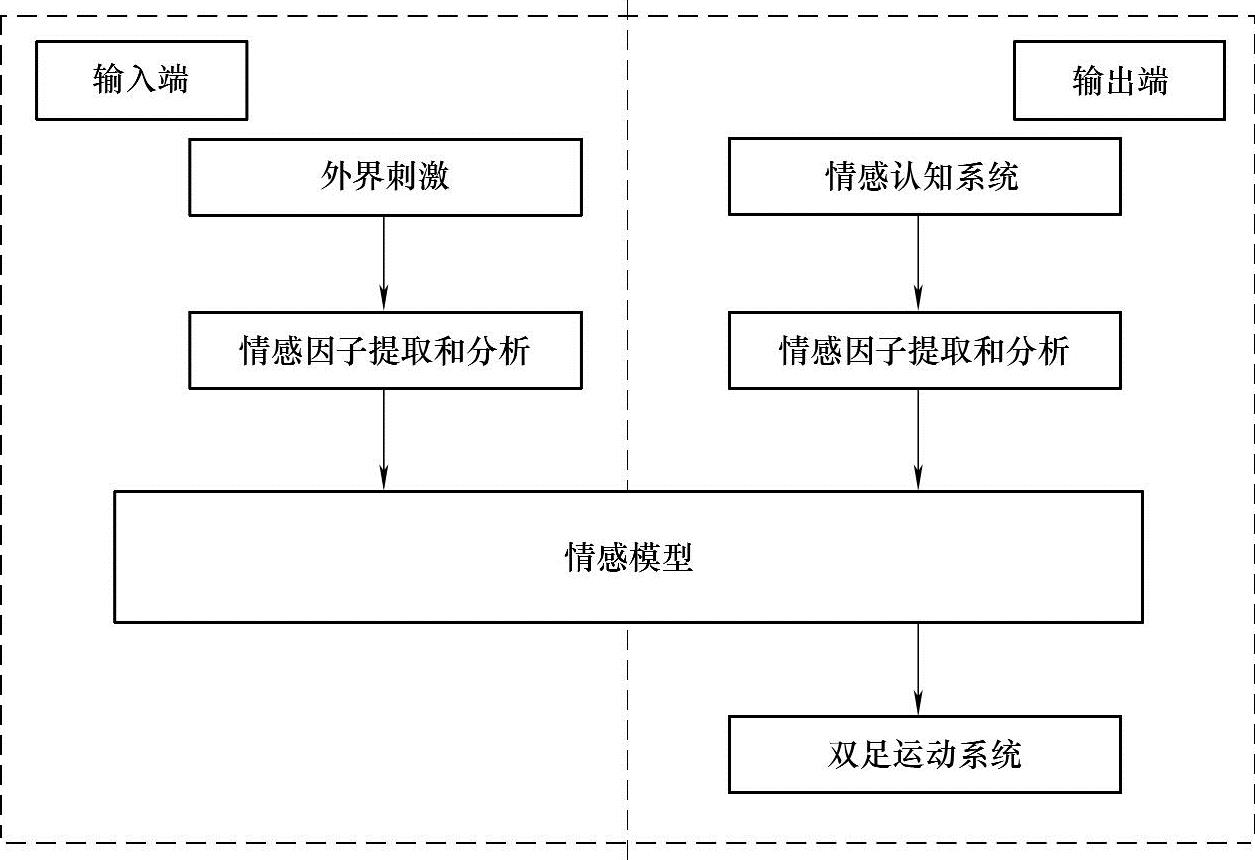
图6-4 情感模型的传递

图6-5 HMM组成示意图

情感熵和情绪熵对π和A的选取也会产生影响，对于某个人而言，在外界刺激变化跨度不大时，其对应某一心理状态的情绪熵数值应基本相等，所以我们假定在3种情感状态（平静、开心、难过）时，给出矩阵A_R和A_P（A_R为开心时的状态概率转移矩阵，A_P为难过时的状态概率转移矩阵）。建立矩阵时要考虑3点约束：

1）符合人类情感规律；

2）符合HMM中马尔可夫链的约束条件，对任意激励均有；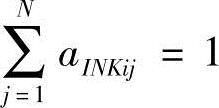

3）要使由HMM构造的个体情绪熵符合个体性格特征。(www.daowen.com)

我们假定当双足机器人未受任何激励作用时的初始概率矢量π为（1，0，0）。我们把外界刺激信号分为导致开心结果的刺激和导致难过结果的刺激两种。这样针对每种刺激分别有一个状态转移概率矩阵（A_R和A_P）及可见符号概率矩阵（B_R和B_P）与之对应。用于模型重估的状态转移概率矩阵及可见符号概率矩阵初始值的选取，可以由经验来决定，同时考虑外界刺激对各个心态下情绪熵的作用。

在接收到开心的刺激时，状态转移概率矩阵为

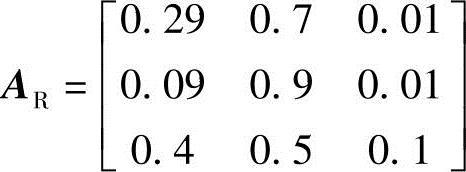
在接收到难过的刺激时，状态转移概率矩阵为

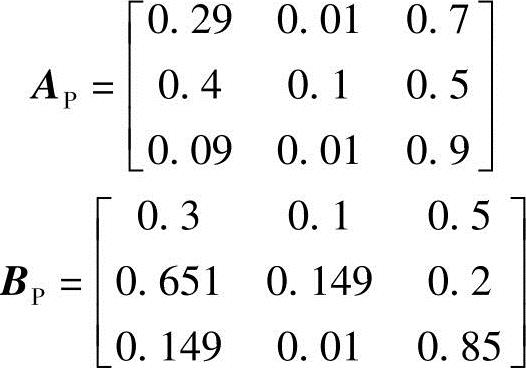
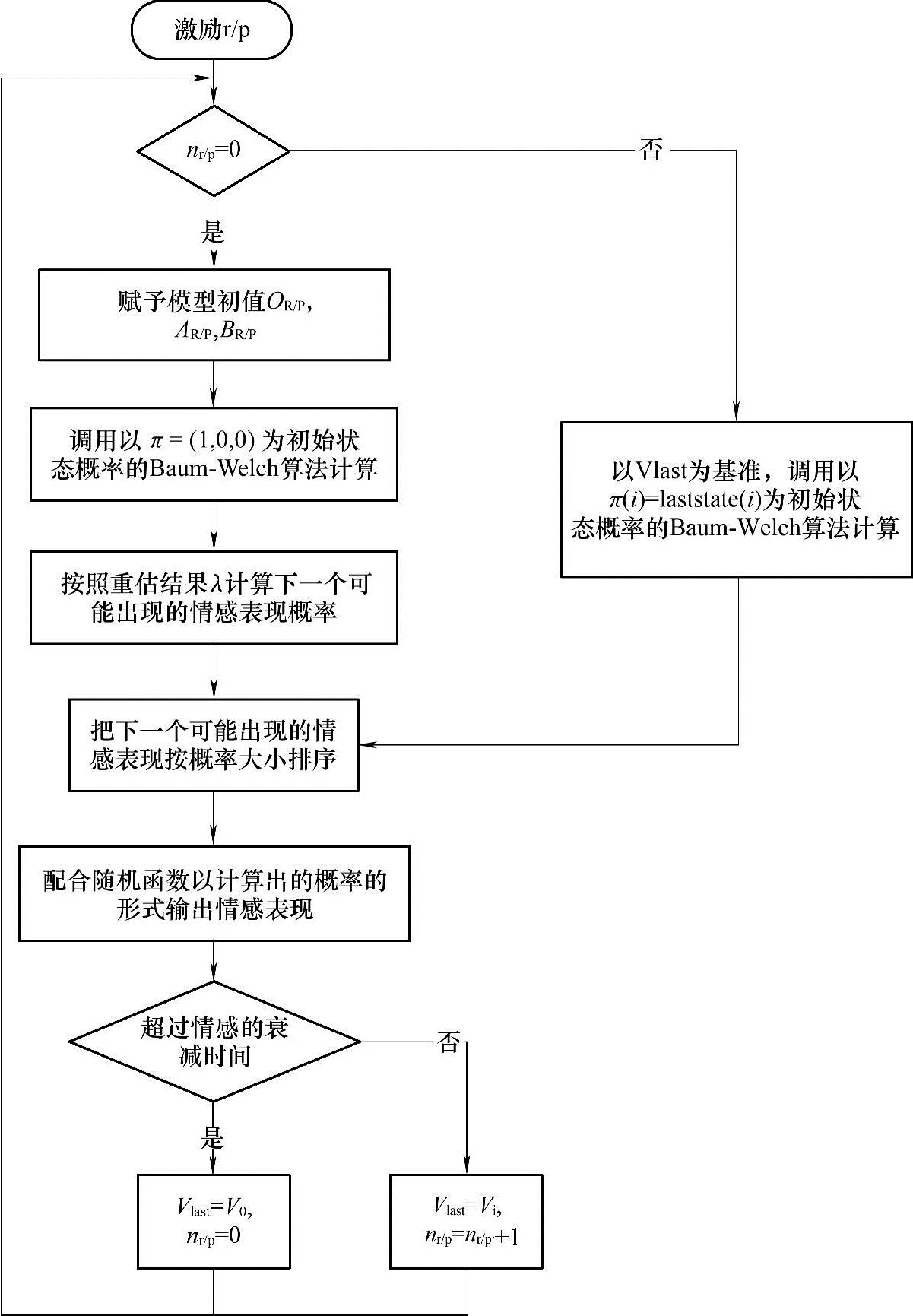
图6-6 基于Baum-Welch算法的程序系统

为了得到充足数据对所有参数进行可靠估计，可以采用多重观察序列，即在实验中多次激励双足机器人，记录在不同激励下得到的双足机器人步态表现，用特定值来表示特定结果。观察序列用二维数组o（l，t）表示，l代表第l个观察序列，t代表观察时刻。此步骤用来调整初始参数，得到给定模型的观察序列概率最大的初始模型参数λ=（A，B，π）。

3.建立结合Baum-Welch算法的程序系统

利用Baum-Welch算法计算情感模型参数的过程为，给出一组训练数据，经过算法程序的运算，可以得到使给定观察序列出现概率局部最大的模型参数估计结果，从而为情感模型参数的确定提供一种理论分析方法。根据刚才提供的初始值和实验中的观察序列训练模型，由最后的模型产生观察序列并且综合考虑行为模式因素和输入信号判断因素的影响，得到如图6-6所示流程图。